Characteristic subgroup

Have questions about this topic? Check out Questions:Characteristic subgroup -- it may already contain your question.

Definition

QUICK PHRASES: invariant under all automorphisms, automorphism-invariant, strongly normal, normal under outer automorphisms

Equivalent definitions in tabular format

Below are many equivalent definitions of characteristic subgroup.

No.	Shorthand	A subgroup of a group is characteristic in it if ...	A subgroup $H$ of a group $G$ is called a characteristic subgroup of $G$ if ...
1	automorphism-invariant	every automorphism of the whole group takes the subgroup to within itself.	for every automorphism $\varphi$ of $G$, $\varphi(H) \subseteq H$. More explicitly, for any $h \in H$ and $\varphi \in \operatorname{Aut}(G)$, $\varphi(h) \in H$.
2	automorphisms restrict to endomorphisms	every automorphism of the group restricts to an endomorphism of the subgroup.	for every automorphism $\varphi$ of $G$, $\varphi(H) \subseteq H$ and $\varphi$ restricts to an endomorphism of $H$.
3	automorphisms restrict to automorphisms	every automorphism of the group restricts to an automorphism of the subgroup.	for every automorphism $\varphi$ of $G$, $\varphi(H) = H$ and $\varphi$ restricts to an automorphism of $H$.
4	(definition in terms of Hom-set maps)	(too complicated to state without symbols)	the image in $\operatorname{Hom}(H,G)$ under the natural map $\operatorname{Aut}(G) \to \operatorname{Hom}(H,G)$ (by restriction) is contained in the image in $\operatorname{Hom}(H,G)$ under the natural map $\operatorname{Aut}(H) \to \operatorname{Hom}(H,G)$ (by inclusion).
5	left transiter of normality	it is normal in any supergroup in which the whole group is normal.	for any group $K$ containing $G$ as a normal subgroup, $H$ is also normal in $K$.

This definition is presented using a tabular format. |View all pages with definitions in tabular format

Notation and terminology

For a subgroup $H \!$ of a group $G \!$, we denote the characteristicity of $\! H$ in $\! G$ by $H \operatorname{char} G$.

Equivalence of definitions

The equivalence of definitions (1) to (4) follows from a more general fact: Restriction of automorphism to subgroup invariant under it and its inverse is automorphism. In other words, we use the fact that both $\varphi$ and $\varphi^{-1}$ send $H$ to within itself to show that $\varphi(H) = H$. It is not in general true that if an automorphism of a group restricts to a subgroup, then the restriction is an automorphism of the subgroup: Restriction of automorphism to subgroup not implies automorphism.

For the equivalence with definition (5), see left transiter of normal is characteristic.

Copyable LaTeX

A subgroup $H$ of a group $G$ is termed a {\em characteristic subgroup} if $\varphi(H) = H$ for all automorphisms $\varphi$ of $G$.

This article is about a basic definition in group theory. The article text may, however, contain advanced material.
VIEW: Definitions built on this | Facts about this: (facts closely related to Characteristic subgroup, all facts related to Characteristic subgroup) |Survey articles about this | Survey articles about definitions built on this
VIEW RELATED: Analogues of this | Variations of this | Opposites of this |[SHOW MORE]

View a complete list of basic definitions in group theory | Go through a guided tour for beginners to this wiki

This article defines a subgroup property that is pivotal (viz important) among existing subgroup properties
View a list of pivotal subgroup properties | View a complete list of subgroup properties[SHOW MORE]

|Get subgroup property lookup help |Get exploration suggestions
VIEW RELATED: Subgroup property implications | Subgroup property non-implications | Subgroup metaproperty satisfactions | Subgroup metaproperty dissatisfactions | Subgroup property satisfactions |Subgroup property dissatisfactions
VIEW FACTS THAT:use, or start with, a subgroup satisfying the property|prove, or show that, a subgroup satisfies the property

This is a variation of normality|Find other variations of normality | Read a survey article on varying normality

Importance

Characteristic subgroups are important because they are genuinely invariant, not just under inner automorphisms, but under all automorphisms. In particular, every subgroup-defining function gives rise to a characteristic subgroup.

Examples

VIEW: subgroups of groups satisfying this property | subgroups of groups dissatisfying this property
VIEW: Related subgroup property satisfactions | Related subgroup property dissatisfactions

Extreme examples

1. Every group is characteristic as a subgroup of itself.
2. The trivial subgroup is characteristic in any group.

Examples in abelian groups

Type of group	High occurrence or low occurrence?	Some or all characteristic subgroups	Explanation/comment
cyclic group	high	every subgroup is characteristic: cyclic implies every subgroup is characteristic	Every subgroup can be described as the set of $d^{th}$ powers for some $d$. This set is invariant under automorphisms.
abelian group	--	the set of $d^{th}$ powers, i.e., elements of the form $x^d$ for fixed integer $d$, variable $x$ (in additive notation, this becomes $dx$)	This set is not just a characteristic subgroup, it is in fact a fully invariant subgroup and a verbal subgroup. See power subgroup.
elementary abelian group, more generally additive group of a field	low	no characteristic subgroups other than trivial subgroup and whole group	The additive group of a field or of a vector space over a field is a group whose automorphism group is transitive on non-identity elements. Hence, it is a characteristically simple group -- any nontrivial characteristic subgroup must be the whole group.

Examples using subgroup-defining functions across all groups

In a non-abelian group, some typical examples of characteristic subgroups are given by subgroup-defining functions (something which uniquely returns a particular subgroup). For instance, we have the following subgroup-defining functions, some of which are interesting for abelian groups as well:

Subgroup-defining function	Definition	Proof of characteristicity
Frattini subgroup	intersection of all maximal subgroups	Frattini subgroup is characteristic
derived subgroup	subgroup generated by all commutators	derived subgroup is characteristic
center	set of elements that commute with every element	center is characteristic

For a complete list of subgroup-defining functions, see Category:Subgroup-defining functions.

Similarly, all terms of the upper central series, lower central series, Frattini series, derived series, Fitting series and other series associated with the group, are characteristic.

For a finite group, any normal Sylow subgroup, and more generally, any normal Hall subgroup, is characteristic. More generally, the normal core of any Sylow subgroup or any Hall subgroup is characteristic.

Examples of subgroups satisfying the property

Here are some examples of subgroups in basic/important groups satisfying the property:

	Group part	Subgroup part	Quotient part
A3 in S3	Symmetric group:S3	Cyclic group:Z3	Cyclic group:Z2

Here are some examples of subgroups in relatively less basic/important groups satisfying the property:

	Group part	Subgroup part	Quotient part
A4 in S4	Symmetric group:S4	Alternating group:A4	Cyclic group:Z2
Center of dihedral group:D8	Dihedral group:D8	Cyclic group:Z2	Klein four-group
Center of quaternion group	Quaternion group	Cyclic group:Z2	Klein four-group
Center of special linear group:SL(2,3)	Special linear group:SL(2,3)	Cyclic group:Z2	Alternating group:A4
Center of special linear group:SL(2,5)	Special linear group:SL(2,5)	Cyclic group:Z2	Alternating group:A5
Cyclic maximal subgroup of dihedral group:D8	Dihedral group:D8	Cyclic group:Z4	Cyclic group:Z2
First agemo subgroup of direct product of Z4 and Z2	Direct product of Z4 and Z2	Cyclic group:Z2	Klein four-group
First omega subgroup of direct product of Z4 and Z2	Direct product of Z4 and Z2	Klein four-group	Cyclic group:Z2
Klein four-subgroup of alternating group:A4	Alternating group:A4	Klein four-group	Cyclic group:Z3
Normal Klein four-subgroup of symmetric group:S4	Symmetric group:S4	Klein four-group	Symmetric group:S3

Here are some examples of subgroups in even more complicated/less basic groups satisfying the property:

	Group part	Subgroup part	Quotient part
Center of M16	M16	Cyclic group:Z4	Klein four-group
Center of dihedral group:D16	Dihedral group:D16	Cyclic group:Z2	Dihedral group:D8
Center of direct product of D8 and Z2	Direct product of D8 and Z2	Klein four-group	Klein four-group
Center of semidihedral group:SD16	Semidihedral group:SD16	Cyclic group:Z2	Dihedral group:D8
Cyclic maximal subgroup of dihedral group:D16	Dihedral group:D16	Cyclic group:Z8	Cyclic group:Z2
Cyclic maximal subgroup of semidihedral group:SD16	Semidihedral group:SD16	Cyclic group:Z8	Cyclic group:Z2
D8 in SD16	Semidihedral group:SD16	Dihedral group:D8	Cyclic group:Z2
Derived subgroup of M16	M16	Cyclic group:Z2	Direct product of Z4 and Z2
Derived subgroup of dihedral group:D16	Dihedral group:D16	Cyclic group:Z4	Klein four-group
Direct product of Z4 and Z2 in M16	M16	Direct product of Z4 and Z2	Cyclic group:Z2
Klein four-subgroup of M16	M16	Klein four-group	Cyclic group:Z4
Non-central Z4 in M16	M16	Cyclic group:Z4	Cyclic group:Z4
Q8 in SD16	Semidihedral group:SD16	Quaternion group	Cyclic group:Z2
SL(2,3) in GL(2,3)	General linear group:GL(2,3)	Special linear group:SL(2,3)	Cyclic group:Z2

Examples of subgroups not satisfying the property

Here are some examples of subgroups in basic/important groups not satisfying the property:

	Group part	Subgroup part	Quotient part
S2 in S3	Symmetric group:S3	Cyclic group:Z2
Z2 in V4	Klein four-group	Cyclic group:Z2	Cyclic group:Z2

Here are some some examples of subgroups in relatively less basic/important groups not satisfying the property:

	Group part	Subgroup part	Quotient part
A3 in A4	Alternating group:A4	Cyclic group:Z3
A3 in A5	Alternating group:A5	Cyclic group:Z3
A3 in S4	Symmetric group:S4	Cyclic group:Z3
A4 in A5	Alternating group:A5	Alternating group:A4
Cyclic maximal subgroups of quaternion group	Quaternion group	Cyclic group:Z4	Cyclic group:Z2
D8 in A6	Alternating group:A6	Dihedral group:D8
D8 in S4	Symmetric group:S4	Dihedral group:D8
Klein four-subgroup of alternating group:A5	Alternating group:A5	Klein four-group
Klein four-subgroups of dihedral group:D8	Dihedral group:D8	Klein four-group	Cyclic group:Z2
Non-characteristic order two subgroups of direct product of Z4 and Z2	Direct product of Z4 and Z2	Cyclic group:Z2	Cyclic group:Z4
Non-normal Klein four-subgroups of symmetric group:S4	Symmetric group:S4	Klein four-group
Non-normal subgroups of dihedral group:D8	Dihedral group:D8	Cyclic group:Z2
S2 in S4	Symmetric group:S4	Cyclic group:Z2
Subgroup generated by double transposition in symmetric group:S4	Symmetric group:S4	Cyclic group:Z2
Twisted S3 in A5	Alternating group:A5	Symmetric group:S3
Z4 in direct product of Z4 and Z2	Direct product of Z4 and Z2	Cyclic group:Z4	Cyclic group:Z2

Here are some examples of subgroups in even more complicated/less basic groups not satisfying the property:

	Group part	Subgroup part	Quotient part
2-Sylow subgroup of general linear group:GL(2,3)	General linear group:GL(2,3)	Semidihedral group:SD16
D8 in D16	Dihedral group:D16	Dihedral group:D8	Cyclic group:Z2
Non-normal subgroups of M16	M16	Cyclic group:Z2

Metaproperties

BEWARE! This section of the article uses terminology local to the wiki, possibly without giving a full explanation of the terminology used (though efforts have been made to clarify terminology as much as possible within the particular context)

Here is a summary:

Metaproperty name	Satisfied?	Proof	Difficulty level (0-5)	Statement with symbols
transitive subgroup property	Yes	characteristicity is transitive	1	If $H\le K \le G$ are groups such that $H$ is characteristic in $K$ and $K$ is characteristic in $G$, then $H$ is characteristic in $G$.
trim subgroup property	Yes	obvious reasons	0	$\{ e \}$ and $G$ are characteristic in $G$
strongly intersection-closed subgroup property	Yes	characteristicity is strongly intersection-closed	1	If $H_i, i \in I$, are all characteristic in $G$, so is the intersection of subgroups $\bigcap_{i \in I} H_i$.
strongly join-closed subgroup property	Yes	characteristicity is strongly join-closed	1	If $H_i, i \in I$, are all characteristic in $G$, so is the join of subgroups $\langle H_i \rangle_{i \in I}$.
quotient-transitive subgroup property	Yes	characteristicity is quotient-transitive	1	If $H \le K \le G$, with $H$ characteristic in $G$ and $K/H$ characteristic in $G/H$, then $K$ is characteristic in $G$.
intermediate subgroup condition	No	characteristicity does not satisfy intermediate subgroup condition	2	We can have $H \le K \le G$ such that $H$ is characteristic in $G$ but $H$ is not characteristic in $K$.
upper join-closed subgroup property	No	characteristicity is not upper join-closed	3	We can have $H \le G$ and $K_1, K_2$ intermediate subgroups such that $H$ is characteristic in both $K_1$ and $K_2$ but not in $\langle K_1, K_2 \rangle$.
commutator-closed subgroup property	Yes	characteristicity is commutator-closed	1	If $H,K$ are characteristic in $G$, so is $[H,K]$.
centralizer-closed subgroup property	Yes	characteristicity is centralizer-closed	1	If $H$ is characteristic in $G$, so is $C_G(H)$.
lower central series condition	No	characteristicity does not satisfy lower central series condition		(second member case): It is possible to have a group $G$ and a characteristic subgroup $H$ such that the derived subgroup $H'$ is not characteristic inside the derived subgroup $G'$.
finite direct power-closed subgroup property	No	characteristicity is not finite direct power-closed	3	($n = 2$ case): It is possible to have a group $G$ and a characteristic subgroup $H$ such that $H \times H$ is not a characteristic subgroup of $G \times G$.
finite-relative-intersection-closed subgroup property	No	characteristicity is not finite-relative-intersection-closed	2	It is possible to have a group $G$ with subgroups $H,K,L$, such that $H \le L, K \le L$, $H$ characteristic in $G$ and $K$ characteristic in $L$, but $H \cap K$ not characteristic in $G$.
partition difference condition	Yes	characteristicity satisfies partition difference condition	1	Suppose $G$ is a group and $H$ is a subgroup of $G$ with a partition into two or more subgroups $H_i, i \in I$. Then, if all except possibly one of the $H_i$s are characteristic subgroups of $G$, all the $H_i$s are characteristic subgroups of $G$.
conditionally lattice-determined subgroup property	No	No subgroup property between normal Sylow and subnormal or between Sylow retract and retract is conditionally lattice-determined		It is possible to have a group $G$, an automorphism $\varphi$ of the lattice of subgroups, and a normal Sylow subgroup $H$ of $G$ such that $\varphi(H)$ is not subnormal. In particular, $H$ is characteristic in $G$ and $\varphi(H)$ is not.

Relation with other properties

This property is a pivotal (important) member of its property space. Its variations, opposites, and other properties related to it and defined using it are often studied

Some of these can be found at:

• Variations of characteristic subgroup
• Analogues of characteristic subgroup in other algebraic structures

Stronger properties

The most important stronger properties are fully invariant subgroup (invariant under all endomorphisms) and isomorph-free subgroup (no other isomorphic subgroup).

Property	Meaning	Proof of implication	Proof of strictness (reverse implication failure)	Intermediate notions	Collapse
fully invariant subgroup (also called fully characteristic subgroup)	invariant under all endomorphisms	fully invariant implies characteristic	characteristic not implies fully invariant (see also list of examples)	Finite direct power-closed characteristic subgroup, Injective endomorphism-invariant subgroup, Normality-preserving endomorphism-invariant subgroup, Retraction-invariant characteristic subgroup, Strictly characteristic subgroup|FULL LIST, MORE INFO	group in which every characteristic subgroup is fully invariant
isomorph-containing subgroup	contains all isomorphic subgroups	isomorph-containing implies characteristic	characteristic not implies isomorph-containing (see also list of examples)	Injective endomorphism-invariant subgroup, Intermediately characteristic subgroup, Intermediately injective endomorphism-invariant subgroup|FULL LIST, MORE INFO	group in which every characteristic subgroup is isomorph-containing
isomorph-free subgroup	no other isomorphic subgroups	(via isomorph-containing)	(via isomorph-containing) (see also list of examples)	Characteristic-isomorph-free subgroup, Injective endomorphism-invariant subgroup, Intermediately characteristic subgroup, Intermediately injective endomorphism-invariant subgroup, Isomorph-containing subgroup, Isomorph-normal characteristic subgroup, Normal-isomorph-free subgroup, Series-isomorph-free subgroup, Sub-(isomorph-normal characteristic) subgroup, Sub-isomorph-free subgroup|FULL LIST, MORE INFO	group in which every characteristic subgroup is isomorph-free
injective endomorphism-invariant subgroup	invariant under injective endomorphisms		characteristic not implies injective endomorphism-invariant	|FULL LIST, MORE INFO
strictly characteristic subgroup	invariant under surjective endomorphisms			|FULL LIST, MORE INFO
homomorph-containing subgroup	contains all homomorphic images	(via isomorph-containing)	(via isomorph-containing) (see also list of examples)	Fully invariant subgroup, Intermediately characteristic subgroup, Intermediately fully invariant subgroup, Intermediately injective endomorphism-invariant subgroup, Intermediately strictly characteristic subgroup, Isomorph-containing subgroup, Normal-homomorph-containing subgroup, Sub-homomorph-containing subgroup|FULL LIST, MORE INFO
subhomomorph-containing subgroup	contains all homomorphic images of subgroups	(via isomorph-containing)	(via isomorph-containing) (see also list of examples)	Fully invariant subgroup, Homomorph-containing subgroup, Intermediately fully invariant subgroup, Isomorph-containing subgroup, Normal-homomorph-containing subgroup, Normal-subhomomorph-containing subgroup, Right-transitively homomorph-containing subgroup, Right-transitively isomorph-containing subgroup, Sub-homomorph-containing subgroup, Subisomorph-containing subgroup, Transfer-closed fully invariant subgroup|FULL LIST, MORE INFO
variety-containing subgroup	contains all subgroups in variety generated	(via isomorph-containing)	(via isomorph-containing)	Fully invariant subgroup, Homomorph-containing subgroup, Intermediately fully invariant subgroup, Isomorph-containing subgroup, Normal-homomorph-containing subgroup, Right-transitively homomorph-containing subgroup, Right-transitively isomorph-containing subgroup, Subhomomorph-containing subgroup, Subisomorph-containing subgroup, Transfer-closed characteristic subgroup, Transfer-closed fully invariant subgroup|FULL LIST, MORE INFO
quotient-isomorph-containing subgroup	contained in any subgroup with isomorphic quotient	quotient-isomorph-containing implies characteristic	characteristic not implies quotient-isomorph-containing (see also list of examples)	|FULL LIST, MORE INFO
quotient-isomorph-free subgroup	no other subgroup with isomorphic quotient	(via quotient-isomorph-containing)	(via quotient-isomorph-containing)	Fully invariant subgroup, Homomorph-containing subgroup, Intermediately fully invariant subgroup, Isomorph-containing subgroup, Normal-homomorph-containing subgroup, Right-transitively homomorph-containing subgroup, Right-transitively isomorph-containing subgroup, Subhomomorph-containing subgroup, Subisomorph-containing subgroup, Transfer-closed characteristic subgroup, Transfer-closed fully invariant subgroup|FULL LIST, MORE INFO
quotient-subisomorph-containing subgroup	contained in any subgroup with quotient isomorphic to a subgroup of its quotient	(via quotient-isomorph-containing)	(via quotient-isomorph-containing)	Fully invariant subgroup, Quotient-isomorph-containing subgroup, Weakly image-closed characteristic subgroup, Weakly image-closed fully invariant subgroup|FULL LIST, MORE INFO
elementarily characteristic subgroup	no other subgroup equivalent in first-order theory of groups	elementarily characteristic implies characteristic	characteristic not implies elementarily characteristic	Monadic second-order characteristic subgroup|FULL LIST, MORE INFO
purely definable subgroup	can be defined using first-order language of groups	(via elementarily characteristic)	(via elementarily characteristic)	Elementarily characteristic subgroup, Monadic second-order characteristic subgroup, Purely definably generated subgroup|FULL LIST, MORE INFO
MSO-definable subgroup	can be defined using monadic second-order language	(via elementarily characteristic)	(via elementarily characteristic)	|FULL LIST, MORE INFO
intermediately characteristic subgroup	characteristic in every intermediate subgroup	obvious	characteristicity does not satisfy intermediate subgroup condition	Intersection of finitely many intermediately characteristic subgroups|FULL LIST, MORE INFO
transfer-closed characteristic subgroup	intersection with any subgroup is characteristic in that subgroup	obvious	(via intermediately characteristic)	Intermediately characteristic subgroup|FULL LIST, MORE INFO
verbal subgroup	defined as elements expressible using a set of words	via fully invariant	(via fully invariant)	Bound-word subgroup, Finite direct power-closed characteristic subgroup, Fully invariant subgroup, Image-closed characteristic subgroup, Image-closed fully invariant subgroup, Intersection of finitely many verbal subgroups, Pseudoverbal subgroup, Quasiverbal subgroup, Quotient-subisomorph-containing subgroup, Weakly image-closed characteristic subgroup, Weakly image-closed fully invariant subgroup|FULL LIST, MORE INFO
existentially bound-word subgroup	defined as set of solutions to existentially bound system of equations	via fully invariant		Bound-word subgroup, Fully invariant subgroup|FULL LIST, MORE INFO
bound-word subgroup	defined as set of solutions to system of equations	via strictly characteristic		Finite direct power-closed characteristic subgroup, Strictly characteristic subgroup|FULL LIST, MORE INFO
finite direct power-closed characteristic subgroup	any finite direct power of the subgroup is characteristic in the corresponding finite direct power of the whole group	(by definition)	characteristicity is not finite direct power-closed	|FULL LIST, MORE INFO
direct power-closed characteristic subgroup	any direct power of the subgroup is closed in the corresponding direct power of the whole group	(by definition)	(via finite direct power-closed characteristic)	Finite direct power-closed characteristic subgroup|FULL LIST, MORE INFO
quasiautomorphism-invariant subgroup	invariant under all quasiautomorphisms	quasiautomorphism-invariant implies characteristic	characteristic not implies quasiautomorphism-invariant	Strong quasiautomorphism-invariant subgroup|FULL LIST, MORE INFO
1-automorphism-invariant subgroup	invariant under all 1-automorphisms			Quasiautomorphism-invariant subgroup|FULL LIST, MORE INFO

For a complete list of subgroup properties stronger than Characteristic subgroup, click here
STRONGER PROPERTIES SATISFYING SPECIFIC METAPROPERTIES: transitive | intermediate subgroup condition | transfer condition | quotient-transitive |intersection-closed |join-closed | trim | inverse image condition | image condition | centralizer-closed |
STRONGER PROPERTIES DISSATISFYING SPECIFIC METAPROPERTIES: transitive | intermediate subgroup condition | transfer condition | quotient-transitive |intersection-closed |join-closed | trim | inverse image condition | image condition | centralizer-closed |

Invariance properties for automorphisms, endomorphisms, and related

Invariance properties and uniqueness properties

Invariance properties and uniqueness properties

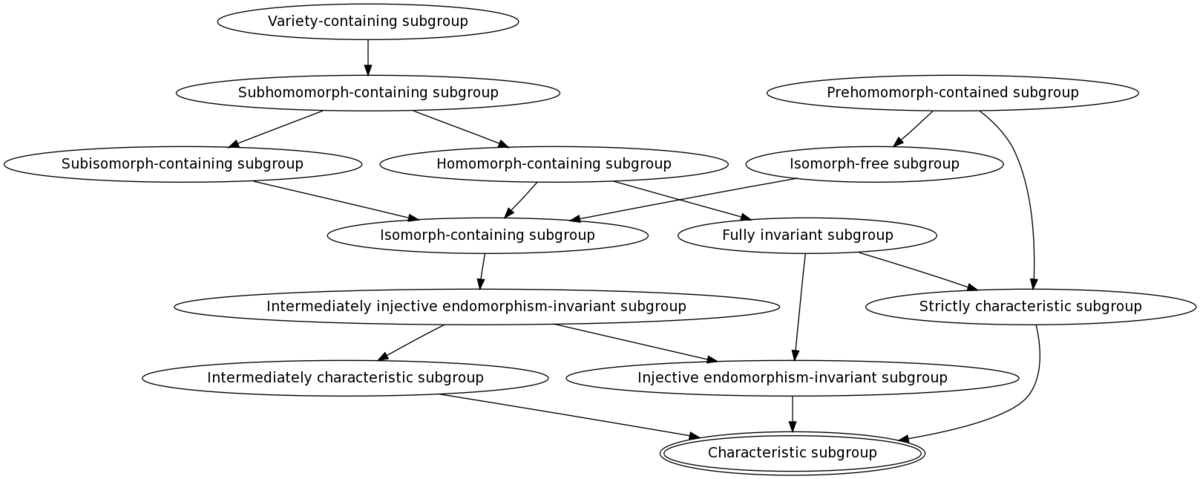
Conjunction with other properties

Important conjunctions of characteristicity with other subgroup properties (Note that multiple properties listed in the second column indicate that any one of them can be used):

Conjunction	Other component of conjunction	Intermediate notions	Additional comments
characteristic central factor	central factor	Characteristic transitively normal subgroup, Conjugacy-closed characteristic subgroup|FULL LIST, MORE INFO
conjugacy-closed characteristic subgroup	conjugacy-closed subgroup or conjugacy-closed normal subgroup	Characteristic transitively normal subgroup|FULL LIST, MORE INFO
characteristic transitively normal subgroup	transitively normal subgroup or CEP-subgroup	|FULL LIST, MORE INFO
characteristic subgroup of finite index	subgroup of finite index or normal subgroup of finite index	Characteristic core of subgroup of finite index, Powering-invariant characteristic subgroup, Quotient-powering-invariant characteristic subgroup|FULL LIST, MORE INFO

View a complete list of conjunctions of characteristicity with subgroup properties

Here are important conjunctions of the property of being a characteristic subgroup with group properties:

Conjunction	Other component of conjunction	Intermediate notions	Additional comments
abelian characteristic subgroup	abelian group	Class two characteristic subgroup, LCS-characteristic subgroup, Nilpotent characteristic subgroup, Solvable characteristic subgroup|FULL LIST, MORE INFO
nilpotent characteristic subgroup	nilpotent group	Solvable characteristic subgroup|FULL LIST, MORE INFO
cyclic characteristic subgroup	cyclic group	Abelian characteristic subgroup, Class two characteristic subgroup|FULL LIST, MORE INFO
solvable characteristic subgroup	solvable group	|FULL LIST, MORE INFO
finite characteristic subgroup	finite group	Powering-invariant characteristic subgroup, Quotient-powering-invariant characteristic subgroup|FULL LIST, MORE INFO
perfect characteristic subgroup	perfect group	|FULL LIST, MORE INFO
simple characteristic subgroup	simple group	|FULL LIST, MORE INFO

View a complete list of conjunctions of characteristicity with group properties

In some cases, we are interested in studying characteristic subgroups where the big group is constrained to satisfy some group property. For instance:

Conjunction	Property of the group	Intermediate notions	Additional comments
characteristic subgroup of finite group	finite group	Elementarily characteristic subgroup, Finite characteristic subgroup, Injective endomorphism-quotient-balanced subgroup, Purely definable subgroup, Purely definably generated subgroup|FULL LIST, MORE INFO
characteristic subgroup of abelian group	abelian group	Abelian characteristic subgroup, Characteristic central subgroup, Characteristic subgroup of center, Powering-invariant characteristic subgroup, Quotient-powering-invariant characteristic subgroup|FULL LIST, MORE INFO
subgroup of cyclic group	cyclic group	|FULL LIST, MORE INFO	in a cyclic group, every subgroup is characteristic
characteristic subgroup of finite abelian group	finite abelian group	|FULL LIST, MORE INFO
characteristic subgroup of nilpotent group	nilpotent group	|FULL LIST, MORE INFO
characteristic subgroup of group of prime power order	group of prime power order	|FULL LIST, MORE INFO
characteristic subgroup of solvable group	solvable group	|FULL LIST, MORE INFO

Weaker properties

Property	Meaning	Proof of implication	Proof of strictness (reverse implication failure)	Intermediate notions	Collapse
normal subgroup	invariant under inner automorphisms (comparison at characteristic versus normal)	characteristic implies normal	normal not implies characteristic (see also list of examples)	Center-fixing automorphism-invariant subgroup, Characteristic subgroup of direct factor, Characteristic-potentially characteristic subgroup, Cofactorial automorphism-invariant subgroup, IA-automorphism-invariant subgroup, Normal-extensible automorphism-invariant subgroup, Normal-potentially characteristic subgroup, Normal-potentially relatively characteristic subgroup, Semi-strongly image-potentially characteristic subgroup, Strongly image-potentially characteristic subgroup, Upper join of characteristic subgroups|FULL LIST, MORE INFO	group in which every normal subgroup is characteristic
subnormal subgroup	chain from subgroup to group, each normal in next	(via normal)	(via normal) (see also list of examples)	Direct factor of characteristic subgroup, Left-transitively fixed-depth subnormal subgroup, Normal subgroup, Normal subgroup of characteristic subgroup, Sub-cofactorial automorphism-invariant subgroup, Subgroup-cofactorial automorphism-invariant subgroup|FULL LIST, MORE INFO	group in which every normal subgroup is characteristic
cofactorial automorphism-invariant subgroup	invariant under all automorphisms whose order's prime factors all divide group's order		(see also list of examples)	|FULL LIST, MORE INFO
coprime automorphism-invariant subgroup	invariant under automorphisms of coprime order			|FULL LIST, MORE INFO
coprime automorphism-invariant normal subgroup	normal and coprime automorphism-invariant			|FULL LIST, MORE INFO
left-transitively 2-subnormal subgroup	if whole group is 2-subnormal in bigger group, so is subgroup	characteristic implies left-transitively 2-subnormal	left-transitively 2-subnormal not implies characteristic (see also list of examples)	Cofactorial automorphism-invariant subgroup, Sub-cofactorial automorphism-invariant subgroup, Subgroup-cofactorial automorphism-invariant subgroup|FULL LIST, MORE INFO
left-transitively fixed-depth subnormal subgroup	for some $k$, if whole group is $k$-subnormal in bigger group, so is subgroup	characteristic of normal implies normal	(via left-transitively 2-subnormal) (see also list of examples)	Left-transitively 2-subnormal subgroup|FULL LIST, MORE INFO
automorph-conjugate subgroup	conjugate to every automorphic subgroup	characteristic implies automorph-conjugate	automorph-conjugate not implies characteristic (see also list of examples)	Intersection-transitively automorph-conjugate subgroup, Join-transitively automorph-conjugate subgroup, Procharacteristic subgroup, Weakly procharacteristic subgroup|FULL LIST, MORE INFO
core-characteristic subgroup	normal core is characteristic in whole group	characteristic subgroup equals its normal core	(via automorph-conjugate) (see also list of examples)	Automorph-conjugate subgroup, Intersection of automorph-conjugate subgroups, Intersection-transitively automorph-conjugate subgroup, Join-transitively automorph-conjugate subgroup|FULL LIST, MORE INFO
closure-characteristic subgroup	normal closure is characteristic in whole group	characteristic subgroup equals its normal closure	(via automorph-conjugate) (see also list of examples)	Automorph-conjugate subgroup, Intersection-transitively automorph-conjugate subgroup, Join-transitively automorph-conjugate subgroup|FULL LIST, MORE INFO
procharacteristic subgroup	conjugate to any automorphic subgroup within the join of the two	characteristic implies procharacteristic	procharacteristic not implies characteristic (see also list of examples)	|FULL LIST, MORE INFO

For a complete list of subgroup properties weaker than Characteristic subgroup, click here
WEAKER PROPERTIES SATISFYING SPECIFIC METAPROPERTIES: transitive | intermediate subgroup condition | transfer condition | quotient-transitive |intersection-closed |join-closed | trim | inverse image condition | image condition | centralizer-closed |
WEAKER PROPERTIES DISSATISFYING SPECIFIC METAPROPERTIES: transitive | intermediate subgroup condition | transfer condition | quotient-transitive |intersection-closed |join-closed | trim | inverse image condition | image condition | centralizer-closed |

Invariance properties and uniqueness properties

Normal-to-characteristic properties

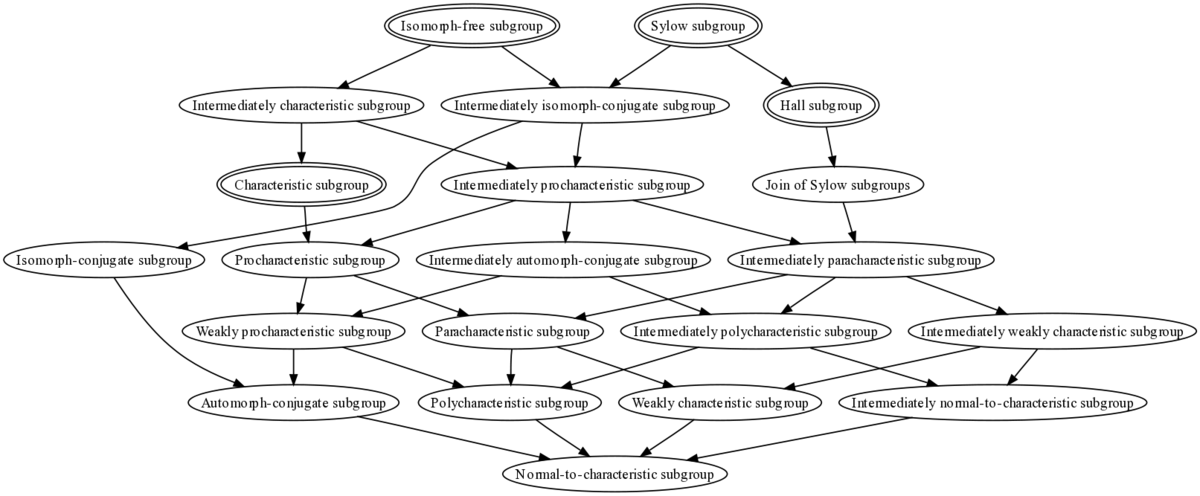
Relation with normality

• Characteristic versus normal: Compares the subgroup properties of characteristicity and normality.
• Between normal and characteristic and beyond: A survey of the subgroup properties lying between normality and characteristicity. Get a list of all intermediate properties here.
• Subnormal-to-normal and normal-to-characteristic: A survey article on subgroup properties such that any normal subgroup satisfying that property is also characteristic.

Analogues in other algebraic structures

Algebraic structure	Analogue of characteristic subgroup in that structure	Definition	Nature of analogy with characteristic subgroup
Lie ring	characteristic Lie subring	A subring of a Lie ring that is invariant under all automorphisms of the whole Lie ring.	Same idea of subalgebra and automorphisms, but for Lie ring structure instead of group structure.
Lie ring	characteristic ideal of a Lie ring	A subring of a Lie ring that arises as the kernel of a homomorphism and is invariant under all automorphisms	Note that since characteristic implies normal, the characteristic subgroups coincide with the characteristic normal subgroups
variety of algebras (universal algebra)	characteristic subalgebra	subalgebra that is invariant under all automorphisms	same definition, applied to an arbitrary algebraic structure.
loop	characteristic subloop	subloop that is invariant under all automorphisms	same definition, applied to another algebraic stricture.

Effect of property operators

BEWARE! This section of the article uses terminology local to the wiki, possibly without giving a full explanation of the terminology used (though efforts have been made to clarify terminology as much as possible within the particular context)

Operator	Meaning	Result of application	Proof
potentially operator	characteristic in some larger group	normal subgroup	normal equals potentially characteristic
simple group operator	no proper nontrivial characteristic subgroup	characteristically simple group
image-potentially operator	exists as the image of a characteristic subgroup via a surjective homomorphism	normal subgroup	normal equals image-potentially characteristic
intermediately operator	characteristic in every intermediate group	intermediately characteristic subgroup
transfer condition operator	intersection with every subgroup is characteristic in it	transfer-closed characteristic subgroup
image condition operator	image for every surjective homomorphism is characteristic in the image	image-closed characteristic subgroup

Formalisms

BEWARE! This section of the article uses terminology local to the wiki, possibly without giving a full explanation of the terminology used (though efforts have been made to clarify terminology as much as possible within the particular context)

Varietal formalism

The notion of characteristic subgroup can be defined as the notion of characteristic subalgebra in the variety of groups.

Second-order description

This subgroup property is a second-order subgroup property, viz., it has a second-order description in the theory of groups
View other second-order subgroup properties

The second-order description of characteristicity is as follows. We say $H$ is characteristic in $G$ if:

$\ \forall g \in H, \sigma \in \operatorname{Aut}(G) : \ \sigma(g) \in H$

The key point is that quantification over $\operatorname{Aut}(G)$ is a second-order quantification.

Function restriction expression

This subgroup property is a function restriction-expressible subgroup property: it can be expressed by means of the function restriction formalism, viz there is a function restriction expression for it.
Find other function restriction-expressible subgroup properties | View the function restriction formalism chart for a graphic placement of this property

Function restriction expression	$H$ is a characteristic subgroup of $G$ if ...	This means that characteristicity is ...	Additional comments
automorphism $\to$ function	every automorphism of $G$ sends every element of $H$ to within $H$	the invariance property for automorphisms
automorphism $\to$ endomorphism	every automorphism of $G$ restricts to an endomorphism of $H$	the endo-invariance property for automorphisms; i.e., it is the invariance property for automorphism, which is a property stronger than the property of being an endomorphism
automorphism $\to$ automorphism	every automorphism of $G$ restricts to a automorphism of $H$	the balanced subgroup property for automorphisms	Hence, it is a t.i. subgroup property, both transitive and identity-true

Relation implication expression

This subgroup property is a relation implication-expressible subgroup property: it can be defined and viewed using a relation implication expression
View other relation implication-expressible subgroup properties

Characteristicity can be expressed in the relation implication formalism with the left side being automorphs (i.e., subgroups resembling each other via an automorphism of the whole group) and the right side being equal subgroups:

Characteristic = Automorphic subgroups $\implies$ Equal subgroups

In other words, a subgroup is characteristic if and only if every subgroup equivalent to it in the sense of being an automorph, is actually equal to it.

Testing

The testing problem

Further information: characteristicity testing problem

Given generating sets for a group and a subgroup, the problem of determining whether the subgroup is characteristic in the group cannot be solved directly. However, it can be reduced to the problem of finding a small generating set for the automorphism group of the bigger group.

GAP command

This subgroup property can be tested using built-in functionality of Groups, Algorithms, Programming (GAP).
The GAP command for testing this subgroup property is:IsCharacteristicSubgroup
The GAP command for listing all subgroups with this property is:CharacteristicSubgroups
View subgroup properties testable with built-in GAP command|View subgroup properties for which all subgroups can be listed with built-in GAP commands | View subgroup properties codable in GAP
Learn more about using GAP

The GAP syntax for testing whether a subgroup is characteristic in a group is:

IsCharacteristicSubgroup (group, subgroup);

where subgroup and group may be defined on the spot in terms of generators or may refer to things defined previously.

The list of all characteristic subgroups can be obtained by:

CharacteristicSubgroups(group);

State of discourse

Mathematical subject classification

Under the Mathematical subject classification, the study of this notion comes under the class: 20A05

Broadly speaking, "characteristic subgroups" are not a separate area of study in group theory, but rather, characteristic subgroups are an important part of the vocabulary that comes up in any sufficiently "pure" study of group theory. Characteristic subgroups are relatively less important in the study of group actions, and more important in the study of abstract group structure.

History

This term was introduced by: Ferdinand Georg Frobenius

The notion of characteristic subgroup was introduced by Frobenius in 1895. His motivation was to capture the property of being a subgroup that is invariant under all symmetries of the group, and is hence intrinsic to the group. Frobenius wanted to use the term invariant subgroup but at the time, the term invariant subgroup was used for normal subgroup.

Resolution of questions that are easy to formulate

Any typical question about the behavior of characteristic subgroups in arbitrary groups that is easy to formulate will also be easy to resolve either with a proof or a counterexample, unless some other feature of the question significantly complicates it. This is so, despite the fact that there are a large number of easy-to-formulate questions about the automorphism group that are still open. The reason is that even though not enough is known about the automorphism groups, there are other ways to obtain information about the structure of characteristic subgroups.

At the one extreme, there are abelian groups, where the characteristic subgroups are quite easy to get a handle on. At the other extreme, there are "all groups" where very little can be said about characteristic subgroups beyond what can be proved through elementary reasoning. The most interesting situation is in the middle, for instance, when we are looking at nilpotent groups and solvable groups. In these cases, there are some restrictions on the structure of characteristic subgroups, but the exact nature of the restrictions is hard to work out.

Below are listed some of the more cutting-edge questions that are relatively easy to formulate and are partially open.

Problem description	More details
potentially characteristic subgroups characterization problem	This problem (or rather, constellation of problems) asks, given a subgroup $H \le G$, whether there exists a group $K$ containing $G$ such that $H$ is characteristic in $K$. Questions of this type are generally much harder to resolve than formulate.
characteristic not implies powering-invariant in nilpotent group	This disproves the conjecture that if $H$ is a characteristic subgroup of a nilpotent group $G$, then $H$ is a powering-invariant subgroup of $G$, i.e., if $G$ is powered over a prime $p$ (unique $p$-divisibility), so is $H$.
Bryant-Kovacs theorem	This theorem provides a "rigidification" result that guarantees the existence of finite p-groups with specific patterns of characteristic subgroups containing the Frattini subgroup.

References

Historical references

• (unknown) by Ferdinand Georg Frobenius, Berliner Sitzungsberichte, (Year 1895): ^{More info}, Page 183
• Theory of Groups of Finite Order by William Burnside, published 1911, Page 92, ^{More info}: The terminology and language in this book is antiquated, and is only of historical interest. View on Google Books

Textbook references

Advanced undergraduate/beginning graduate algebra texts:

Book	Page number	Chapter and section	Contextual information	View
Abstract Algebra by David S. Dummit and Richard M. Foote, 10-digit ISBN 0471433349, 13-digit ISBN 978-0471433347More info	135	Section 4.4 (Automorphisms)	formal definition
Topics in Algebra by I. N. HersteinMore info	70	Problem 7(a)	introduced in exercise
Algebra by Michael Artin, ISBN 0130047635, 13-digit ISBN 978-0130047632More info	234	Section 8 (generators and relations), Exercise 7	introduced in exercise
A First Course in Abstract Algebra (6th Edition) by John B. Fraleigh, ISBN 0201763907More info	428	Exercises 8.6, Concepts, Point 4	introduced in exercise
Contemporary Abstract Algeba by Joseph Gallian, ISBN 0618514716More info	168
Basic Algebra: Groups, Rings, and Fields by Paul Moritz Cohn, ISBN 1852335874, 13-digit ISBN 978-1852335878More info	46	Section 2.6	definition in paragraph tangential to the topic of discussion.	Google Books
Algebra (Graduate Texts in Mathematics) by Thomas W. Hungerford, ISBN 0387905189More info	103	Chapter II, Section 7	definition in paragraph precursor to results using the idea.	Google Books

Graduate texts on group theory:

Book	Page number	Chapter and section	Contextual information	View
Finite Group Theory by I. Martin Isaacs, ISBN 0821843443, 13-digit ISBN 978-0821843444More info	11		definition in paragraph	Google Books
Groups and representations by Jonathan Lazare Alperin and Rowen B. Bell, ISBN 0387945261More info	17		formal definition in paragraph	Google Books
Nilpotent groups and their automorphisms by Evgenii I. Khukhro, ISBN 3110136724More info	4	Section 1.1	definition in paragraph with a few important facts about characteristic and normal subgroups.
Finite Group Theory (Cambridge Studies in Advanced Mathematics) by Michael Aschbacher, ISBN 0521786754More info	25			Google Books
A Course in the Theory of Groups by Derek J. S. Robinson, ISBN 0387944613More info	28	Section 1.5	definition in paragraph	Google Books
An introduction to the theory of groups by Joseph J. Rotman, ISBN 0387942858, 13-digit ISBN 978-0387942858More info	104		formal definition	Google Books

Online lecture notes

• J.S. Milne's course notes, Section 3.2, Page 41 (both the A4 and the letter version)