Subnormal-to-normal and normal-to-characteristic

This survey article is about the following three kinds of subgroup properties:

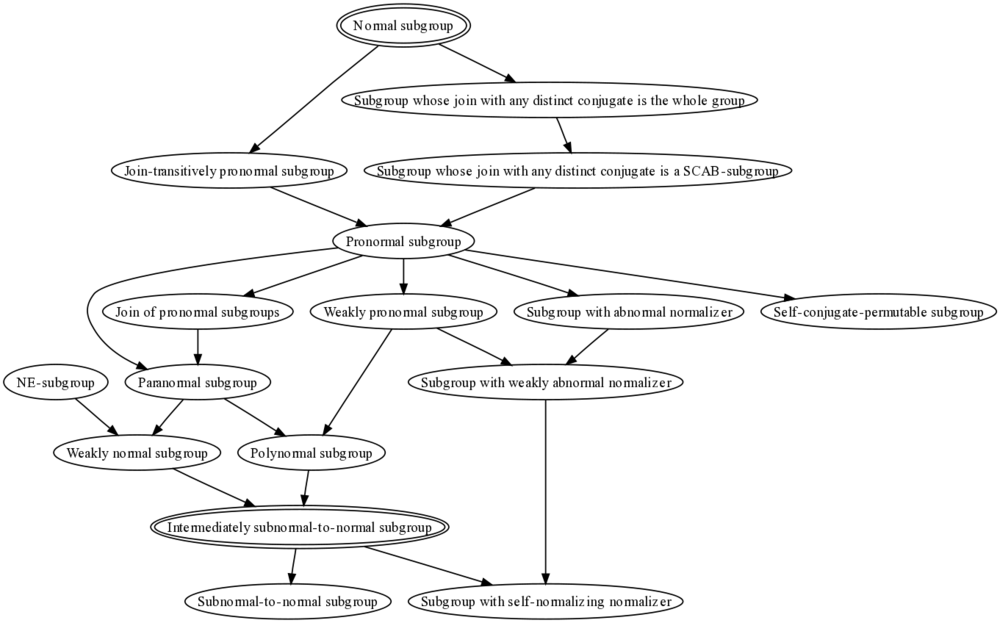
• Subgroup properties $p$ that are stronger than the property of being a subnormal-to-normal subgroup. These properties behave as follows: Any subnormal subgroup having the property $p$ is a normal subgroup. Most of the properties we discuss here are stronger than the property of being an intermediately subnormal-to-normal subgroup: a subgroup satisfying property $p$ has the property that if it is subnormal in any intermediate subgroup, it is also normal in that intermediate subgroup.
• Subgroup properties $p$ that are stronger than the property of being a normal-to-characteristic subgroup. These properties behave as follows: any normal subgroup having the property $p$ is a characteristic subgroup. Most of the properties we discuss here are stronger than the property of being an intermediately normal-to-characteristic subgroup: a subgroup satisfying property $p$ has the property that if it is normal in any intermediate subgroup, it is also characteristic in that intermediate subgroup.
• Subgroup properties such that the only normal subgroup satisfying the property is the whole group (called NCI-subgroup properties on the wiki).

Subnormal-to-normal properties

General remarks

• Most of the properties we discuss here satisfy the intermediate subgroup condition. A subgroup property $p$ satisfies the intermediate subgroup condition if whenever $H\leq K\leq G$ are such that $H$ satisfies $p$ in $G$, $H$ also satisfies $p$ in $K$.
• Most of the properties here are satisfied by all normal subgroups, and also by all maximal subgroups. None of them is transitive, and in fact, the subordination of any of these properties (i.e., the transitive closed with respect to inclusion) is usually satisfied for all subgroups of finite groups. (The reason for the lack of transitivity in general can be traced to the fact that subgroup property between normal and subnormal-to-normal is not transitive).
• Most of the properties here are not closed under intersections. Some are closed under joins, and many are closed under normalizing joins. A subgroup property is normalizing join-closed if whenever $H,K\leq G$ are such that both $H,K$ satisfy $p$ and $K\leq N_{G}(H)$, the join $\langle H,K\rangle =HK$ also satisfies $p$.

We will follow a right-action convention to denote conjugation. Thus, $H^{g}=g^{-1}Hg$, will be termed the conjugate of $H$ by $g$. In the left-action convention, $c_{g}(H)=gHg^{-1}$ is the conjugate of $H$ by $g$. To use the left-action convention, replace $g$ by $g^{-1}$ and reverse the order of terms in products.

Pronormal subgroup

Further information: Pronormal subgroup

A subgroup $H$ of a group $G$ is termed pronormal in $G$ if, for any $g\in G$, there exists $x\in \langle H,H^{g}\rangle$ such that $H^{x}=H^{g}$.

Any normal subgroup is pronormal, and any maximal subgroup is pronormal. More generally, there are several properties between the property of being normal or maximal and the property of being pronormal. Here are some of them:

• Subgroup whose join with any distinct conjugate is the whole group: Both normal and maximal subgroups satisfy this property, and this property in turn is stronger than pronormality. For full proof, refer: Join with any distinct conjugate is the whole group implies pronormal
• Subgroup whose join with any distinct conjugate is a SCAB-subgroup: This is weaker than the previous property, but still stronger than the property of being pronormal.

Pronormality behaves very differently from normality. Some salient facts about it:

• Pronormality satisfies intermediate subgroup condition: Any pronormal subgroup of the whole group is pronormal in every intermediate subgroup.
• Pronormal and subnormal implies normal, Pronormal implies intermediately subnormal-to-normal: A pronormal subgroup that is subnormal in any intermediate subgroup is also normal in that intermediate subgroup.
• Pronormality is not finite-join-closed (a join of pronormal subgroups need not be pronormal), but pronormality is normalizing join-closed: If $H,K$ are pronormal subgroups of $G$ and $K\leq N_{G}(H)$, then $HK$ is a pronormal subgroup.
• Pronormality is not transitive. A right-transitively pronormal subgroup is a subgroup $K\leq G$ such that any pronormal subgroup of $K$ is pronormal in $G$. Any direct factor, central factor, or more generally, any SCAB-subgroup is a right-transitively pronormal subgroup. For full proof, refer: SCAB implies right-transitively pronormal
• Pronormality satisfies image condition: The image of a pronormal subgroup under a surjective homomorphism of groups is surjective in the image.
• Pronormal implies WNSCDIN. Pronormal implies MWNSCDIN: Pronormal subgroups satisfy a strong condition on conjugacy of normal subsets. Any two normal subsets of a pronormal subgroup that are conjugate in the whole group are conjugate in the normalizer of the pronormal subgroup.
• Pronormal implies self-conjugate-permutable: The only conjugate of a pronormal subgroup that permutes with it is itself.

As we shall see further ahead, Sylow subgroups, and more generally, Sylow subgroups of normal subgroups, are pronormal. In fact, many results proved about Sylow subgroups generalize to results about pronormal subgroups.

Weakly pronormal subgroup

Further information: Weakly pronormal subgroup

The condition of being a weakly pronormal subgroup is a slight weakening of the condition of being a pronormal subgroup. Here, instead of looking at the subgroup generated by $H$ and one conjugate $H^{g}$, we look at the subgroup generated by $H$ and the conjugates of $H$ by all powers of $g$. This subgroup is denoted $H^{\langle g\rangle }$. We require that there exist $x\in H^{\langle g\rangle }$ such that $H^{x}=H^{g}$.

Paranormal subgroup

Further information: Paranormal subgroup

Paranormality is a weakening of pronormality, but in a somewhat different direction. For pronormality, we insist that there exist $x\in \langle H,H^{g}\rangle$ such that $H^{x}=H^{g}$. For paranormality, we weaken this from requiring the existence of a single element to simply requiring that $H$ be a contranormal subgroup inside $\langle H,H^{g}\rangle$: in other words, we require that the normal closure of $H$ in $\langle H,H^{g}\rangle$ be $\langle H,H^{g}\rangle$.

Here are some salient facts about paranormality:

• Paranormality satisfies intermediate subgroup condition
• Paranormal implies intermediately subnormal-to-normal
• Paranormality is strongly join-closed: The join of an arbitrary collection of paranormal subgroups is paranormal.
• Paranormality satisfies image condition
• Pronormal implies paranormal, Paranormal not implies pronormal

Polynormal subgroup

Further information: Polynormal subgroup

Polynormality is a weakening of pronormality that combines the previous two weakenings. $H$ is polynormal in $G$ if, for any $g\in G$, $H$ is a contranormal subgroup of $\langle H,H^{g}\rangle$.

Pronormality implies both paranormality and weak pronormality, and both of these imply polynormality. No example of a finite group is known where a polynormal subgroup is not paranormal.

Here are some salient facts about polynormality:

• Polynormality satisfies intermediate subgroup condition
• Polynormal implies intermediately subnormal-to-normal
• Polynormality satisfies image condition
• Polynormality is strongly join-closed

Weakly normal subgroup

Further information: Weakly normal subgroup

Weak normality is an extremely weak condition; it is weaker than paranormality, though possibly not weaker than polynormality. A subgroup $H$ of a group $G$ is termed weakly normal in $G$ if for any $g\in G$, $H^{g}\leq N_{G}(H)$ implies $H^{g}\leq H$.

Some salient facts about weak normality:

• Weak normality satisfies intermediate subgroup condition
• Weakly normal implies intermediately subnormal-to-normal
• Paranormal implies weakly normal, Weakly normal not implies paranormal

NE-subgroup

Further information: NE-subgroup

The condition of being a NE-subgroup is stronger than weak normality, but is incomparable with paranormality, pronormality, or weak pronormality. Every normal subgroup as well as every self-normalizing subgroup (we'll see more on those later) is a NE-subgroup.

A subgroup $H$ of a group $G$ is termed a NE-subgroup if $H$ equals the intersection of its normalizer and normal closure in $G$.

Some salient facts about NE-subgroups:

• NE satisfies intermediate subgroup condition
• NE implies weakly normal, NE implies intermediately subnormal-to-normal
• NE not implies paranormal, Sylow not implies NE, pronormal not implies NE, paranormal not implies NE

Intermediately subnormal-to-normal subgroup

Further information: intermediately subnormal-to-normal subgroup, image-closed intermediately subnormal-to-normal subgroup

A subgroup $H$ of a group $G$ is termed intermediately subnormal-to-normal in $G$ if whenever $K$ is a subgroup of $G$ containing $H$, and $H$ is a subnormal subgroup of $K$, $H$ is also a normal subgroup of $K$. This is equivalent to demanding that whenever $H$ is a 2-subnormal subgroup of $K$, $H$ is normal in $K$.

All the properties mentioned above are stronger than the property of being intermediately subnormal-to-normal.

The property of being intermediately subnormal-to-normal does not satisfy the image condition. In other words, a surjective homomorphism need not send intermediately subnormal-to-normal subgroups to intermediately subnormal-to-normal subgroups. A subgroup whose image under any surjective homomorphism is an intermediately subnormal-to-normal subgroup of the whole image is termed an image-closed intermediately subnormal-to-normal subgroup.

Note: The concept of intermediately subnormal-to-normal was referred to in one paper as transitively normal while the concept of image-closed intermediately subnormal-to-normal was referred to in the same paper as strong transitively normal.

Subgroup with self-normalizing normalizer, abnormal normalizer, and weakly abnormal normalizer

Further information: subgroup with self-normalizing normalizer, subgroup with abnormal normalizer, subgroup with weakly abnormal normalizer

A subgroup $H$ of a group $G$ is termed a subgroup with self-normalizing normalizer if $N_{G}(N_{G}(H))=N_{G}(H)$. It turns out that any intermediately subnormal-to-normal subgroup has a self-normalizing normalizer.

We can, however, have non-normal 2-subnormal subgroups, and more generally, subnormal subgroups of arbitrarily large subnormal depth, that have self-normalizing normalizers. Closely related is the property of being a subgroup with abnormal normalizer (the normalizer of the subgroup is an abnormal subgroup), and being a subgroup with weakly abnormal normalizer (the normalizer of the subgroup is a weakly abnormal subgroup). Some important facts:

• Normalizer of pronormal implies abnormal: In particular, a pronormal subgroup is a subgroup with abnormal normalizer.
• Normalizer of weakly pronormal implies weakly abnormal
• Normalizer of intermediately subnormal-to-normal implies self-normalizing
• Abnormal normalizer and 2-subnormal not implies normal: The property of having an abnormal normalizer is insufficient to guarantee that the subgroup is subnormal-to-normal.

Normal-to-characteristic and normal-to-isomorph-free properties

General remarks

For this part, we shall follow the convention of automorphisms acting on the right, by exponentiation. This is to keep consistent with the notation of conjugation on the right. To convert these to analogous statements with automorphisms acting on the left, simply interchange the order of terms in all products.

The properties discussed here are of the kind that, whenever any normal subgroup satisfies the property, it must be a characteristic subgroup. Some of the properties here are even stronger: they are such that whenever any normal subgroup satisfies them, it must be an isomorph-free subgroup.

Some of these properties have this behavior in intermediate subgroups as well: whenever a subgroup with the property is normal in an intermediate subgroup, it is characteristic (or isomorph-free) in that intermediate subgroup.

One of the things that makes the implications messier is that characteristicity does not satisfy intermediate subgroup condition: in other words, a subgroup that is characteristic in the whole group need not be characteristic in every intermediate subgroup. On the other hand, the property of being an isomorph-free subgroup does satisfy the intermediate subgroup condition.

Isomorph-free subgroup, isomorph-containing subgroup

Further information: isomorph-free subgroup, isomorph-containing subgroup

A subgroup $H$ of a group $G$ is termed an isomorph-free subgroup if any subgroup of $G$ isomorphic to $H$ is actually equal to $H$. $H$. is termed an isomorph-containing subgroup of $G$ if any subgroup of $G$ isomorphic to $H$ is contained in $H$.

For finite subgroups, and more generally for co-Hopfian subgroups, the two properties are equivalent.

Some salient points about these properties:

• Both these properties satisfy the intermediate subgroup condition. In other words, if $H\leq K\leq G$ and $H$ satisfies the property in $G$, $H$ also satisfies the property in $K$.
• Both these properties are stronger than the property of being a characteristic subgroup. In particular, they imply the property of being an intermediately characteristic subgroup: being characteristic in every intermediate subgroup.

Isomorph-conjugate and automorph-conjugate subgroups

Further information: isomorph-conjugate subgroup, automorph-conjugate subgroup

We say that $H$ is isomorph-conjugate in $G$ if any subgroup of $G$ isomorphic to $H$ is conjugate to $H$. Similarly, we say that $H$ is automorph-conjugate in $G$ if any subgroup of $G$ that is automorphic to $H$ (i.e., is the image of $H$ under an automorphism of $G$) is conjugate to $H$.

We have the following:

• Neither the property of being isomorph-conjugate nor the property of being automorph-conjugate satisfy the intermediate subgroup condition. In other words, we can have $H\leq K\leq G$ such that $H$ is isomorph-conjugate in $G$ but not in $K$.
• Every isomorph-free subgroup is isomorph-conjugate, and any characteristic subgroup is automorph-conjugate.
• For a normal subgroup, being isomorph-conjugate is equivalent to being isomorph-free, and being automorph-conjugate is equivalent to being characteristic.

Intermediately characteristic, intermediately isomorph-conjugate and intermediately automorph-conjugate

Further information: intermediately characteristic subgroup, intermediately isomorph-conjugate subgroup, intermediately automorph-conjugate subgroup

We define the following for a subgroup $H$ of a group $G$:

• $H$ is intermediately characteristic in $G$ if $H$ is characteristic in every intermediate subgroup.
• $H$ is intermediately isomorph-conjugate in $G$ if $H$ is isomorph-conjugate in every intermediate subgroup.
• $H$ is intermediately automorph-conjugate in $G$ if $H$ is automorph-conjugate in every intermediate subgroup.

Notice that, since any normal subgroup that is automorph-conjugate (resp., isomorph-conjugate) is in fact characteristic (resp., isomorph-free), each of these properties is stronger than the property of being an intermediately normal-to-characteristic subgroup.

Procharacteristic and weakly procharacteristic

Further information: procharacteristic subgroup, weakly procharacteristic subgroup, intermediately procharacteristic subgroup

Procharacteristicity is something like being automorph-conjugate in every intermediate subgroup, except that it is somewhat different. For the definition of procharacteristicity, we require that the automorphism be only in the ambient group, while conjugacy be checked in intermediate subgroups. Specifically:

A subgroup $H$ of a group $G$ is termed procharacteristic if, for any automorphism $\sigma$ of $G$, there exists $x\in \langle H,H^{\sigma }\rangle$ such that $H^{x}=H^{\sigma }$.

We have a similar definition for a weakly procharacteristic subgroup:

A subgroup $H$ of a group $G$ is termed procharacteristic if, for any automorphism $\sigma$ of $G$, there exists $x\in \langle H^{\langle }\sigma \rangle$ such that $H^{x}=H^{\sigma }$.

Some salient points:

• Any intermediately isomorph-conjugate subgroup is procharacteristic. Any characteristic subgroup is also procharacteristic.
• Procharacteristicity does not satisfy the intermediate subgroup condition. A subgroup that is procharacteristic in every intermediate subgroup is termed an intermediately procharacteristic subgroup. Any intermediately characteristic subgroup, and any intermediately isomorph-conjugate subgroup, is intermediately procharacteristic.
• An intermediately automorph-conjugate subgroup need not be procharacteristic. Conversely, a procharacteristic subgroup need not be intermediately automorph-conjugate. Further information: Intermediately automorph-conjugate not implies procharacteristic
• An intermediately automorph-conjugate subgroup must be weakly procharacteristic. In fact, a subgroup is intermediately automorph-conjugate if and only if it is weakly procharacteristic in every intermediate subgroup.
• Any weakly procharacteristic subgroup, and hence any procharacteristic subgroup, is an automorph-conjugate subgroup.

Paracharacteristic, polycharacteristic, intermediately paracharacteristic, and intermediately polycharacteristic

Further information: paracharacteristic subgroup, polycharacteristic subgroup, intermediately paracharacteristic subgroup, ntermediately polycharacteristic subgroup

PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]

One of the people editing this page intended to fill in this information at a later stage, but hasn't gotten around to doing it yet. If you see this placeholder for a long time, file an error report at the error reporting page.

Weakly characteristic and intermediately weakly characteristic

Further information: weakly characteristic subgroup, intermediately weakly characteristic subgroup

PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]

One of the people editing this page intended to fill in this information at a later stage, but hasn't gotten around to doing it yet. If you see this placeholder for a long time, file an error report at the error reporting page.

Other properties

There are many other normal-to-characteristic properties of interest. Some of these are discussed below:

• Closure-characteristic subgroup: This is a subgroup whose normal closure is a characteristic subgroup. Any join of automorph-conjugate subgroups has this property, and it is stronger than the property of being a normal-to-characteristic subgroup. The property obtained by applying the intermediately operator to this is the property of being an intermediately closure-characteristic subgroup.
• Core-characteristic subgroup: This is a subgroup whose normal core is a characteristic subgroup. Any intersection of automorph-conjugate subgroups has this property, and it is stronger than the property of being a normal-to-characteristic subgroup. The property obtained by applying the intermediately operator to this is the property of being an intermediately core-characteristic subgroup.

Relating subnormal-to-normal and normal-to-characteristic

The general form of the relation

The properties we discussed in the last two sections: the sort that help us go from subnormal to normal, and the sort that help us go from normal to characteristic, are closely related. They are related by means of the left residual, something we shall try to describe here.

Suppose $p,q,r$ are three subgroup properties. We say that $r$ is the left residual of $p$ by $q$ if we have the following:

A subgroup $H$ of a group $K$ has property $r$ in $K$ if and only if for every $G$ containing $K$ such that $K$ has property $q$ in $G$, $H$ has property $p$ in $G$.

The left residual of a property by itself is termed its left transiter. A basic fact is:

Left transiter of normal is characteristic: A subgroup $H$ of $K$ is characteristic in $K$ if and only if, whenever $K$ is normal in a group $G$, $H$ is normal in $G$.

In our case, we observe that the left residual of a subnormal-to-normal property by the property of being a normal subgroup is a normal-to-characteristic property. If $p$ is the subnormal-to-normal property and $r$ is the normal-to-characteristic property, our general results will be of the form:

• Any subgroup with property $r$ in a normal subgroup has property $p$ in the whole group.
• If $H$ is a subgroup of $K$ such that whenever $K$ is normal in $G$, $H$ is also normal in $G$, $H$ has property $r$ in $K$.

The proofs of all these rely on the fact that inner automorphism to automorphism is right tight for normality. This states that for any group $K$, and any automorphism $\sigma$ of $K$, there exists a group $G$ containing $K$ as a normal subgroup, such that $\sigma$ extends to an inner automorphism of $G$.

Some specific examples of the relation

Subnormal-to-normal property	Left residual, which is a normal-to-characteristic property
Pronormal subgroup	Procharacteristic subgroup
Weakly pronormal subgroup	Weakly procharacteristic subgroup
Paranormal subgroup	Paracharacteristic subgroup
Polynormal subgroup	Polycharacteristic subgroup
Weakly normal subgroup	Weakly characteristic subgroup

In certain situations, we cannot precisely compute the left residual, but can show that a certain property is stronger than the left residual. For instance:

• Intermediately normal-to-characteristic of normal implies intermediately subnormal-to-normal

The left residual of intermediately subnormal-to-normal by normal

Of particular interest is the elusive property $r$ which seems to have no better name than the left residual of intermediately subnormal-to-normal by normal. This is at any rate stronger than being a normal-to-characteristic subgroup, but weaker than being an intermediately normal-to-characteristic subgroup. In fact, all the properties in the diagram of normal-to-characteristic subgroup properties, except the one right at the bottom, are stronger than the left residual of intermediately subnormal-to-normal by normal:

To understand why this is so, observe that the properties at the bottom here are all obtained as left residuals of certain properties by normality, each of which is stronger than the property of being an intermediately subnormal-to-normal subgroup. In particular, a subgroup of a normal subgroup with any of these properties inside the normal subgroup, is intermediately subnormal-to-normal in the whole group.

Application to Sylow and Hall subgroups

Further information: Sylow subgroup, Hall subgroup

Sylow subgroups are particularly important, and the conjugacy part of Sylow's theorem states that all Sylow subgroups for the same prime are conjugate. Further, Sylow satisfies intermediate subgroup condition: any Sylow subgroup of the whole group is also a Sylow subgroup in any intermediate subgroup. Thus, Sylow subgroups are intermediately isomorph-conjugate subgroups, which sits pretty high in the implication chain. Among other things, Sylow subgroups are procharacteristic, weakly procharacteristic, intermediately automorph-conjugate, intermediately core-characteristic, intermediately closure-characteristic, and so on.

Most importantly, any Sylow subgroup of a normal subgroup is pronormal. This follows from the fact that Sylow subgroups are procharacteristic. In particular, Sylow subgroups are themselves pronormal, and this has many ramifications.

Hall subgroups need not be isomorph-conjugate or automorph-conjugate. However, Hall implies join of Sylow subgroups, and thus, Hall subgroups are paracharacteristic subgroups, and in particular, any Hall subgroup of a normal subgroup is paranormal. This allows us to prove a number of things about Hall subgroups as well.

NCI-properties and how they fit in

Contranormal subgroup

Further information: Contranormal subgroup

A subgroup $H$ of a group $G$ is termed contranormal in $G$ if the normal closure of $H$ in $G$ equals $G$.

Here are some facts about contranormality:

• Contranormality is upward-closed: If $H$ is contranormal in $G$, any subgroup of $G$ containing $H$ is also contranormal in $G$.
• Contranormality does not satisfy intermediate subgroup condition: We can have $H\leq K\leq G$ such that $H$ is contranormal in $G$ but $H$ is not contranormal in $K$.
• Contranormality is UL-join-closed: Suppose, for some indexing set $I$, we have subgroups $H_{i}\leq K_{i}\leq G$, with $i\in I$, such that each $H_{i}$ is contranormal in $K_{i}$. Then, the join of the $H_{i}$s is contranormal in the join of the $K_{i}$s.

It is true that the only subgroup that is both normal and contranormal is the whole group. In fact, the only subgroup that is both subnormal and contranormal is the whole group. This is because given any proper subnormal subgroup $H$, there is a subnormal series:

$H=H_{0}\leq H_{1}\leq \dots \leq H_{n}=G$.

The right-most member of this series that is not equal to $G$ is a proper normal subgroup of $G$ containing $H$. Hence, $H$ cannot be contranormal.

Thus, any contranormal subgroup is a subnormal-to-normal subgroup for trivial reasons. However, it is not an intermediately subnormal-to-normal subgroup in general because contranormality does not satisfy the intermediate subgroup condition.

Self-normalizing subgroup

Further information: Self-normalizing subgroup

A subgroup $H$ of a group $G$ is termed self-normalizing if its normalizer $N_{G}(H)$ is equal to $H$. Here are some salient facts about self-normalizing subgroups:

• Self-normalizing is not upward-closed: If $H\leq K\leq G$ are such that $H$ is self-normalizing in $G$, it is not necessary that $K$ be self-normalizing in $G$.
• Self-normalizing satisfies intermediate subgroup condition: A self-normalizing subgroup of a group is also self-normalizing in every intermediate subgroup.
• A self-normalizing subgroup that is also normal (or more generally, subnormal) must be the whole group.
• Self-normalizing implies intermediately subnormal-to-normal: A self-normalizing subgroup that is subnormal in any intermediate subgroup must be equal to the intermediate subgroup, and hence, must be normal in it.

Weakly abnormal subgroup

Further information: Weakly abnormal subgroup

A subgroup $H$ of a group $G$ is termed a weakly abnormal subgroup if it satisfies the following equivalent conditions:

• It is contranormal in every intermediate subgroup.
• Every subgroup containing it is self-normalizing.
• For any $x\in G$, we have $x\in H^{\langle x\rangle }$.

For the equivalence of these definitions, refer: Equivalence of definitions of weakly abnormal subgroup.

Weakly abnormal subgroups are related to weakly pronormal subgroups as follows: a subgroup is weakly abnormal if and only if it is weakly pronormal and self-normalizing. Also, normalizer of weakly pronormal implies weakly abnormal.

Abnormal subgroup

Further information: Abnormal subgroup

The condition of abnormality is somewhat stronger than the condition of weak abnormality. $H$ is abnormal in $G$ if, for every $x\in G$, we have $x\in \langle H,H^{x}\rangle$. Abnormality corresponds to pronormality just as weak abnormality corresponds to weak pronormality. An abnormal subgroup is precisely the same as a self-normalizing pronormal subgroup. Also, normalizer of pronormal implies abnormal.

References

Journal references

• Finite soluble groups with pronormal system normalizers by John S. Rose, Proceedings of the London Mathematical Society, ISSN 1460244X (online), ISSN 00246115 (print), Volume 17, Page 447 - 469(Year 1967): ^{Weblink on Oxford Journals pageMore info}
• Nilpotent self-normalizing subgroups of soluble groups by Roger W. Carter, Math. Zeitschr., Volume 75, Page 136 - 139(Year 1961): ^{WeblinkMore info}
• Nilpotent self-normalizing subgroups and system normalizers by Roger W. Carter, Volume 12, Page 535 - 563(Year 1962): ^{WeblinkMore info}
• Nilpotent subgroups of finite soluble groups by John S. Rose, Math. Zeitschr., Volume 106, Page 97 - 112(Year 1968): ^{WeblinkMore info}
• Pronormality in finite groups by T. A. Peng, Journal of the London Mathematical Society, ISSN 14697750 (online), ISSN 00246107 (print), Volume 3, Page 301 - 306(Year 1971): ^{WeblinkMore info}
• Transitivity of normality and pronormal subgroups by L. A. Kurdachenko and I. Ya. Subbotin, Combinatorial group theory, discrete groups, and number theory, Volume 421, Page 201 - 210(Year 2006): ^{More info}
• Abnormal, pronormal, contranormal, and Carter subgroups in some generalized minimax groups by L. A. Kurdachenko, J. Otal and I. Ya. Subbotin,  : ^{WeblinkMore info}