Thompson's critical subgroup theorem

This article gives the statement, and possibly proof, of a particular subgroup of kind of subgroup in a group being self-centralizing. In other words, the centralizer of the subgroup in the group is contained in the subgroup
View other similar statements

This article gives the statement, and possibly proof, of a particular subgroup of kind of subgroup in a finite group being coprime automorphism-faithful. In other words, any non-identity automorphism of of the whole group, of coprime order to the whole group, that restricts to the subgroup, restricts to a non-identity automorphism of the subgroup.
View other such statements

History

The critical subgroup theorem was first proved in the joint paper on the odd-order theorem by Walter Feit and John Griggs Thompson. The part of the paper containing this theorem (Chapter 2, Lemma 8.2, see also the references below) is generally attributed to Thompson.

The term critical subgroup appeared in Gorenstein's book on Finite Groups (see also the references below).

Statement

General statement

Let $G$ be a group of prime power order, i.e., a finite $p$-group for some prime $p$. Then, $G$ has a critical subgroup, i.e., a characteristic subgroup $H$ satisfying the following four conditions:

1. $\Phi(H) \le Z(H)$, viz., the Frattini subgroup is contained inside the center (i.e., $H$ is a Frattini-in-center group).
2. $[G,H] \le Z(H)$ (i.e., $H$ is a commutator-in-center subgroup of $G$).
3. $C_G(H)= Z(H)$ (i.e., $H$ is a self-centralizing subgroup of $G$).
4. $H$ is coprime automorphism-faithful in $G$: If $\sigma$ is a non-identity automorphism of $G$ such that the order of $\sigma$ is relatively prime to $p$, then the restriction of $\sigma$ to $H$ is a non-identity automorphism of $H$.

Note that since characteristic and self-centralizing implies coprime automorphism-faithful, a characteristic subgroup satisfying condition (3) automatically satisfies condition (4). Thus, it suffices to show conditions (1)-(3).

Related facts

Analogues for other kinds of groups

• Analogue of critical subgroup theorem for finite solvable groups
• Analogue of critical subgroup theorem for infinite abelian-by-nilpotent p-groups

Applications

• Odd-order p-group has coprime automorphism-faithful characteristic class two subgroup of prime exponent
• Classification of finite p-groups of characteristic rank one

Other related facts

• Abelian Frattini subgroup implies centralizer is critical

Analysis

Further information: Analysis of Thompson's critical subgroup theorem

While Thompson's critical subgroup theorem is constructive, it does not necessarily yield all possible critical subgroups. In fact, it yields critical subgroups satisfying two additional constraints: the center is maximal among abelian characteristic subgroups and, moreover, a critical subgroup obtained through this procedure is completely determined by its center, while there may be other critical subgroups with the same center. A critical subgroup that can arise through the constructive procedure of this theorem is termed a constructibly critical subgroup. It turns out that every abelian critical subgroup is constructibly critical.

The fact that there is no unique choice of critical subgroup makes critical subgroups different from other characteristic subgroups we typically encounter. More information is available at analysis of Thompson's critical subgroup theorem.

Facts used

General facts

1. Maximal among abelian normal implies self-centralizing in nilpotent
2. Characteristic and self-centralizing implies coprime automorphism-faithful

Facts about normality

Fact No.	Statement	Explanation
Norm1	Normality satisfies image condition	The image of a normal subgroup, under a surjective homomorphism, or quotient map, is normal.
Norm2	Normality satisfies inverse image condition	The inverse image of a normal subgroup, under any homomorphism, is normal.
Norm3	Normality is centralizer-closed	The centralizer of any normal subgroup is normal.

Facts about characteristicity

The fact numbers given here are for reference in the proof, and have no deeper significance.

Fact no.	Statement	Explanation
Char1	Characteristic implies normal	Every characteristic subgroup is normal
Char2	Characteristicity is quotient-transitive	If $A$ is characteristic in $B$, and $I$ is an intermediate subgroup such that $I/A$ is characteristic in $B/A$, then $I$ is characteristic in $B$
Char3	Characteristicity is transitive	If $A$ is a characteristic subgroup of $B$, and $B$ is a characteristic subgroup of $D$, then $A$ is a characteristic subgroup of $D$
Char4	Characteristicity is strongly intersection-closed	An intersection of characteristic subgroups is characteristic. In particular, if $A,B \le D$ are characteristic subgroups, then $A \cap B$ is also characteristic.
Char5	Characteristicity is centralizer-closed	If $A$ is a characteristic subgroup of $B$, the centralizer $C_B(A)$ is also a characteristic subgroup.

Facts about Omega-1

1. Omega-1 of center is normality-large: For a finite $p$-group $P$, the intersection of $\Omega_1(Z(P))$ with any nontrivial normal subgroup of $P$ is a nontrivial subgroup (in fact, it is a nontrivial normal subgroup).

Proof

This proof uses a tabular format for presentation. Provide feedback on tabular proof formats in a survey (opens in new window/tab) | Learn more about tabular proof formats|View all pages on facts with proofs in tabular format

Given: A finite $p$-group $G$

To prove: $G$ has a critical subgroup.

Note that by fact (2) in the list of general facts (characteristic and self-centralizing implies coprime automorphism-faithful) it suffices to find a characteristic subgroup satisfying conditions (1)-(3).

If there exists a characteristic subgroup maximal among abelian normal subgroups

We first consider the case that there exists a subgroup $M$ of $G$ maximal among Abelian normal subgroups, such that $M$ is also a characteristic subgroup. By fact (1) in the list of general facts, we see that $M$ is a self-centralizing subgroup. We check all the conditions for $M$:

1. Frattini-in-center group condition: $\Phi(M) \le Z(M)$: This condition is satisfied trivially because $M$ is Abelian.
2. Commutator-in-center subgroup conidtion: $[G,M] \le Z(M)$: By normality of $M$, $[G,M] \le M$, and by Abelianness of $M$, $M = Z(M)$. Thus, $[G,M] \le Z(M)$.
3. Self-centralizing subgroup condition: $C_G(M) \le M$: This condition is satisfied by assumption.

In the other case: setting up the subgroups

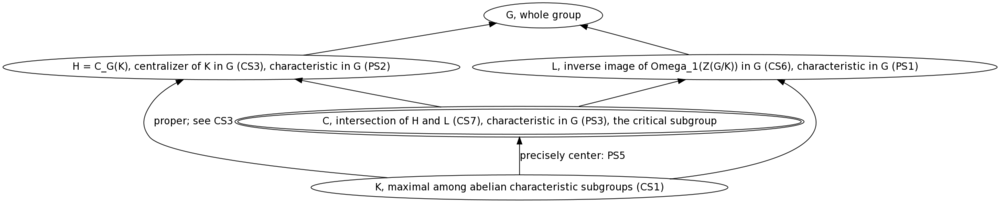
Step no.	Letter introduced	Way of choosing it	Unique choice (given previous choices)?	Relevant observations for subsequent choices
CS1	$\! K$	maximal among abelian characteristic subgroups of $G$	no	Since $K$ is characteristic, it is also, in particular, normal, so $K$ is an abelian normal subgroup of $G$.
CS2	$\! M$	maximal among abelian normal subgroups of $G$ containing $K$	no	$M$ is maximal among abelian normal subgroups, and $K$ is a proper subgroup of $M$.
CS3	$\! H$	$H = C_G(K)$: the centralizer of $K$ in $G$	yes	Since $M$ is abelian and contains $K$, we have $K < M \le H$. In particular, $K < H$.
CS4	$\! \overline{G}$	$\overline{G} = G/K$ is the quotient group by $K$	yes	This is permissible since $K$ is a characteristic subgroup, and by fact (1) on characteristic subgroups, every characteristic subgroup is normal.
CS5	$\! \Omega_1(Z(\overline{G})$	This is the set of elements of order dividing $p$ in the center of $\overline{G}$, and is also the socle of $\overline{G}$.	yes	This is a characteristic subgroup of $\overline{G}$
CS6	$\! L$	The inverse image in $G$ of the $\Omega_1(Z(\overline{G}))$	yes	$L$ contains $K$ and $L/K = \Omega_1(Z(\overline{G})$. We will also denote $L/K$ as $\overline{L}$ to be consistent with the rest of the bar notation.
CS7	$\! C$	$C = H \cap L$	yes	Since $K$ is contained in both $H$ and $L$, $K$ is contained in $C$

We now begin the proof.

Step no.	Assertion	Facts used	Construction steps used	Proof steps used	Explanation
PS1	$L$ is characteristic in $G$	(Char2)	(CS1), (CS5), (CS6)	--	[SHOW MORE] $K$ is characteristic in $G$, and $L/K = \Omega_1(Z(\overline{G}))$ is characteristic in the quotient $\overline{G} = G/K$. Thus, by (Char2) (set: $A = K, I = L, B = G$), $L$ is characteristic in $G$.
PS2	$H$ is characteristic in $G$	(Char5)	(CS1), (CS3)	--	[SHOW MORE] Since $H = C_G(K)$, we have, by (Char5) (set: $A = K, B = G$), that $H$ is characteristic in $G$.
PS3	$C$ is characteristic in $G$	(Char4)	--	(PS1), (PS2)	[SHOW MORE] By (Char4), the subgroup $C = H \cap L$ is characteristic in $G$.
PS4	$Z(C)$ is characteristic in $G$	(Char3)	--	(PS3)	[SHOW MORE] The center $Z(C)$ is a characteristic subgroup of $C$. Thus, by fact (3) (set: $A = Z(C), B = C, D = G$), $Z(C)$ is a characteristic subgroup of $G$.
PS5	$Z(C) = K$	--	(CS1), (CS3), (CS7)	(PS4)	[SHOW MORE] By our choice, $Z(C)$ is an abelian characteristic subgroup of $G$. Further, since $C \le H = C_G(K)$ and $K$ is contained in $C$, $K \le Z(C)$. So $Z(C)$ is an abelian characteristic subgroup of $G$ containing $K$. By maximality of $K$ with respect to being abelian characteristic, $K = Z(C)$.

Proving the conditions for criticality

Our goal is now to show that $C$ satisfies the conditions for being a critical subgroup. Recall that we have established that $C$ is a characteristic subgroup of $G$ and that $Z(C) = K$. Also, recall that:

$H = C_G(K), \overline{H} = H/K, \overline{L} = \Omega_1(Z(\overline{G}), C = H \cap L, \overline{C} = C/K$.

We check the conditions one by one:

1. Frattini-in-center group condition: We need to show that $\Phi(C) \le K$: For this, observe that $\overline{C}$ is contained in $\Omega_1(Z(\overline{G}))$, which is elementary Abelian (it is contained in an Abelian group $Z(G)$, and is generated by elements of order $p$). Thus, $C/K$ is elementary Abelian, and we get $\Phi(C) \le K$.
2. Commutator-in-center subgroup condition: We need to show that $[G,C] \le K$: Modulo $K$, the image of $C$ is contained in $\Omega_1(Z(\overline{G}))$, which is contained in $Z(\overline{G})$. Hence $[\overline{G}, \overline{C}] \le [\overline{G},Z(\overline{G})]$, which is trivial. Hence $[G,C] \le K$.
3. Self-centralizing subgroup condition: We need to show that $C_G(C) \le C$: We do this by contradiction. Since the proof is somewhat long, we do it in the table below.

ASSUMPTION: Suppose $Q = C_G(C)$, such that $Q$ is not in $C$.

Step no.	Assertion	Facts used	Steps used (earlier parts)	Steps used (this part)	Contradiction-prone assumption used?	Explanation
PSC1	$Q$ is normal in $G$	(Char1), (Norm3)	(PS3)	--	no	[SHOW MORE] By (PS3), $C$ is characteristic in $G$, hence by (Char1), $C$ is normal in $G$. By (Norm3), we get that $Q = C_G(C)$ is also normal in $G$.
PSC2	$Q \cap C = K$	--	(PS5)	--	no	[SHOW MORE] By definition, $Q \cap C = C_G(C) \cap C = Z(C)$. We showed that $Z(C) = K$, so $Q \cap C = K$.
PSC3	$\overline{Q} = Q/K$ is nontrivial and normal in $\overline{G}$	(Norm1)	--	(PSC1)	yes	[SHOW MORE] Define $\overline{Q} = Q/K$. By (Norm1), and the fact that $Q$ is normal in $G$, we obtain that $\overline{Q}$ is normal in $\overline{G}$. Also, since $Q$ is not contained in $C$ (by assumption), $K$ is a proper subgroup of $Q$, so $\overline{Q}$ is nontrivial.
PSC4	$\overline{Q} \cap \overline{C}$ is trivial	--	--	(PSC2)	no	[SHOW MORE] $\overline{Q} \cap \overline{C}$ is the same as the image in $G/K$ of $Q \cap C$, because they both contain $K$. By (PSC2), this image is trivial.
PSC5	$\overline{Q}$ intersects $\overline{L}$ nontrivially	fact (1) about Omega-1	--	(PSC3)	yes	[SHOW MORE] Since $\Omega_1(Z(\overline{G}))$ is normality-large in $\overline{G}$ (fact (1) about Omega-1), and $\overline{Q}$ is nontrivial and normal in $\overline{G}$ (by PSC3), we conclude that $\overline{Q}$ must intersect $\Omega_1(Z(\overline{G})) = \overline{L}$ nontrivially.
PSC6	$Q \le H$, and thus, $\overline{Q} \le \overline{H}$	--	--	--	no	[SHOW MORE] Since $K \le C$, we have $Q = C_G(C) \le C_G(K) = H$, so $Q \le H$. Going modulo $K$, we get $\overline{Q} \le \overline{H}$.
PSC7	$\overline{C} = \overline{H} \cap \overline{L}$	--	(CS3), (CS6),(CS7)	--	no	[SHOW MORE] By definition, $C = H \cap L$. Since all three subgroups contain $K$ by definition, the intersection holds when we take quotients by $K$.
PSC8	$\overline{Q} \cap (\overline{H} \cap \overline{L})$ is trivial	--	--	(PSC4), (PSC7)	no	[SHOW MORE] $\overline{Q} \cap (\overline{H} \cap \overline{L}) = \overline{Q} \cap \overline{C}$ by (PSC7). By (PSC4), this intersection is trivial.
PSC9	$(\overline{Q} \cap \overline{H}) \cap \overline{L}$ is nontrivial	--	--	(PSC5), (PSC6)	yes	[SHOW MORE] By (PSC6), $(\overline{Q} \cap \overline{H}) \cap \overline{L} = \overline{Q} \cap \overline{L}$, and (PSC5), this is nontrivial.
PSC10	Contradiction!	--	-	(PSC8) and (PSC9)	yes	[SHOW MORE] (PSC8) claims that a particular triple intersection is trivial, while (PSC9) claims that the same intersection is nontrivial. We thus get a contradiction.

References

Journal references

• Solvability of groups of odd order by Walter Feit and John Griggs Thompson, Pacific Journal of Mathematics, Volume 13, Page 775 - 1029(Year 1963): This 255-page long paper gives a proof that odd-order implies solvable: any odd-order group (i.e., any finite group whose order is odd) is a solvable group.^{Project Euclid pageMore info}: Thompson's critical subgroup theorem appears as Lemma 8.2, Section 8 (Miscellaneous preliminary lemmas) in Chapter 2, Page 795.

Textbook references

• Finite Groups by Daniel Gorenstein, ISBN 0821843427, Page 185, Theorem 3.11 (including Lemma 3.12, also theorem 3.13), Section 5.3, ^{More info}