Subgroup structure of groups of order 16
This article gives specific information, namely, subgroup structure, about a family of groups, namely: groups of order 16.
View subgroup structure of group families | View subgroup structure of groups of a particular order |View other specific information about groups of order 16
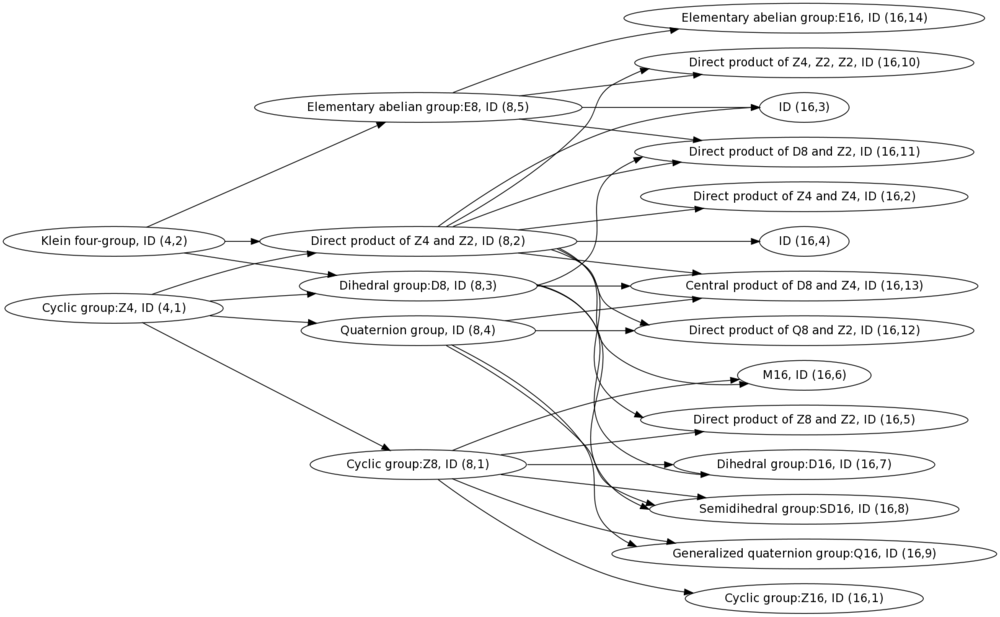
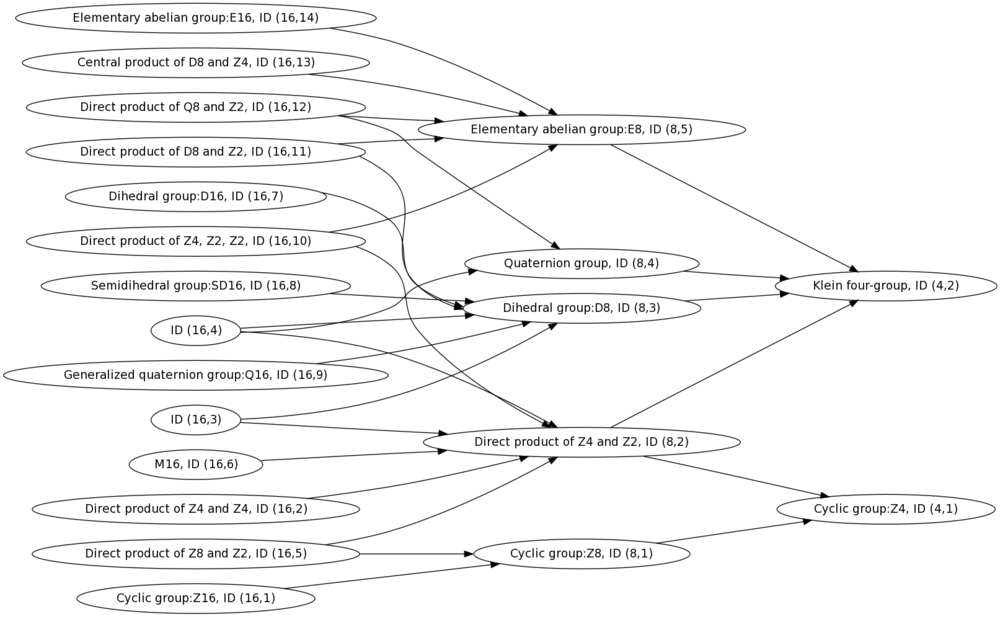
Subgroup/quotient relationships
Subgroup relationships
Quotient relationships
Possibilities for maximal subgroups
Numerical information on counts of subgroups by isomorphism type
FACTS TO CHECK AGAINST FOR SUBGROUP STRUCTURE: (group of prime power order)
Lagrange's theorem (order of subgroup times index of subgroup equals order of whole group, so all subgroups have prime power orders)|order of quotient group divides order of group (and equals index of corresponding normal subgroup, so all quotients have prime power orders)
prime power order implies not centerless | prime power order implies nilpotent | prime power order implies center is normality-large
size of conjugacy class of subgroups divides index of center
congruence condition on number of subgroups of given prime power order: The total number of subgroups of any fixed prime power order is congruent to 1 mod the prime.
Number of subgroups per isomorphism type
The number in each column is the number of subgroups in the given group of that isomorphism type:
| Group | Second part of GAP ID | Hall-Senior number | Hall-Senior symbol | Nilpotency class | cyclic group:Z2 | cyclic group:Z4 | Klein four-group | cyclic group:Z8 | direct product of Z4 and Z2 | dihedral group:D8 | quaternion group | elementary abelian group:E8 | Total (row sum + 2, for trivial group and whole group) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 3 | 6 | 1 | 0 | 3 | 0 | 0 | 0 | 15 | |
| SmallGroup(16,3) | 3 | 9 | 2 | 7 | 4 | 7 | 0 | 2 | 0 | 0 | 1 | 23 | |
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 6 | 1 | 0 | 3 | 0 | 0 | 0 | 15 | |
| direct product of Z8 and Z2 | 5 | 4 | 1 | 3 | 2 | 1 | 2 | 1 | 0 | 0 | 0 | 11 | |
| M16 | 6 | 11 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 0 | 0 | 11 | |
| dihedral group:D16 | 7 | 12 | 3 | 9 | 1 | 4 | 1 | 0 | 2 | 0 | 0 | 19 | |
| semidihedral group:SD16 | 8 | 13 | 3 | 5 | 3 | 2 | 1 | 0 | 1 | 1 | 0 | 15 | |
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 5 | 0 | 1 | 0 | 0 | 2 | 0 | 11 | |
| direct product of Z4 and V4 | 10 | 2 | 1 | 7 | 4 | 7 | 0 | 6 | 0 | 0 | 1 | 27 | |
| direct product of D8 and Z2 | 11 | 6 | 2 | 11 | 2 | 13 | 0 | 1 | 4 | 0 | 2 | 35 | |
| direct product of Q8 and Z2 | 12 | 7 | 2 | 3 | 6 | 1 | 0 | 3 | 0 | 4 | 0 | 19 | |
| central product of D8 and Z4 | 13 | 8 | 2 | 7 | 4 | 3 | 0 | 3 | 3 | 1 | 0 | 23 | |
| elementary abelian group:E16 | 14 | 1 | 1 | 15 | 0 | 35 | 0 | 0 | 0 | 0 | 15 | 67 | |
| Total | -- | -- | -- | -- | 78 | 46 | 76 | 8 | 23 | 10 | 8 | 19 | 296 |
| Average | -- | -- | -- | -- | 5.5714 | 3.2857 | 5.4286 | 0.5714 | 1.6429 | 0.7143 | 0.5714 | 1.3571 | 21.1429 |
Number of normal subgroups per isomorphism type
The number in each column is the number of normal subgroups in the given group of that isomorphism type.
Note that for groups in the same Hall-Senior genus, the total number of normal subgroups is equal, and in fact, the number of subgroups of each order, and even of each Hall-Senior family within an order, is equal. However, the number of subgroups of each specific isomorphism type may not be equal.
| Group | Second part of GAP ID | Hall-Senior number | Hall-Senior symbol | Nilpotency class | cyclic group:Z2 | cyclic group:Z4 | Klein four-group | cyclic group:Z8 | direct product of Z4 and Z2 | dihedral group:D8 | quaternion group | elementary abelian group:E8 | Total (row sum + 2, for trivial group and whole group) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 3 | 6 | 1 | 0 | 3 | 0 | 0 | 0 | 15 | |
| SmallGroup(16,3) | 3 | 9 | 2 | 3 | 0 | 3 | 0 | 2 | 0 | 0 | 1 | 11 | |
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 2 | 1 | 0 | 3 | 0 | 0 | 0 | 11 | |
| direct product of Z8 and Z2 | 5 | 4 | 1 | 3 | 2 | 1 | 2 | 1 | 0 | 0 | 0 | 11 | |
| M16 | 6 | 11 | 2 | 1 | 2 | 1 | 2 | 1 | 0 | 0 | 0 | 9 | |
| dihedral group:D16 | 7 | 12 | 3 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 7 | |
| semidihedral group:SD16 | 8 | 13 | 3 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 7 | |
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 1 | 0 | 1 | 0 | 0 | 2 | 0 | 7 | |
| direct product of Z4 and V4 | 10 | 2 | 1 | 7 | 4 | 7 | 0 | 6 | 0 | 0 | 1 | 27 | |
| direct product of D8 and Z2 | 11 | 6 | 2 | 3 | 2 | 5 | 0 | 1 | 4 | 0 | 2 | 19 | |
| direct product of Q8 and Z2 | 12 | 7 | 2 | 3 | 6 | 1 | 0 | 3 | 0 | 4 | 0 | 19 | |
| central product of D8 and Z4 | 13 | 8 | 2 | 1 | 4 | 3 | 0 | 3 | 3 | 1 | 0 | 17 | |
| elementary abelian group:E16 | 14 | 1 | 1 | 15 | 0 | 35 | 0 | 0 | 0 | 0 | 15 | 67 |
Number of characteristic subgroups per isomorphism type
The number in each column is the number of characteristic subgroups in the given group of that isomorphism type.
| Group | Second part of GAP ID | Hall-Senior number | Hall-Senior symbol | Nilpotency class | cyclic group:Z2 | cyclic group:Z4 | Klein four-group | cyclic group:Z8 | direct product of Z4 and Z2 | dihedral group:D8 | quaternion group | elementary abelian group:E8 | Total (row sum + 2, for trivial group and whole group) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | |
| SmallGroup(16,3) | 3 | 9 | 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | |
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 7 | |
| direct product of Z8 and Z2 | 5 | 4 | 1 | 1 | 2 | 1 | 0 | 1 | 0 | 0 | 0 | 7 | |
| M16 | 6 | 11 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 0 | 0 | 7 | |
| dihedral group:D16 | 7 | 12 | 3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | |
| semidihedral group:SD16 | 8 | 13 | 3 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 7 | |
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | |
| direct product of Z4 and V4 | 10 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | |
| direct product of D8 and Z2 | 11 | 6 | 2 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 5 | |
| direct product of Q8 and Z2 | 12 | 7 | 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 4 | |
| central product of D8 and Z4 | 13 | 8 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 5 | |
| elementary abelian group:E16 | 14 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
Numerical information on counts of subgroups by order
Number of subgroups per order
- Due to congruence condition on number of subgroups of given prime power order, all the counts of subgroups, as well as of normal subgroups, are odd.
- Since index two implies normal, we have, in all cases, that the number of subgroups of order 8 = number of normal subgroups of order 8. See also equivalence of definitions of maximal subgroup of group of prime power order.
- Formula for number of maximal subgroups of group of prime power order: The subgroups of order 8 (all of which are normal) correspond to the maximal subgroups of the Frattini quotient, which is an elementary abelian group of order . The number of such subgroups is , and hence must be one of the numbers 1,3,7,15.
- Formula for number of minimal normal subgroups of group of prime power order: The normal subgroups of order 2 correspond precisely to the subgroups of order 2 in the socle, which is an elementary abelian subgroup defined as of the center. If the socle has order , the number of normal subgroups of order 2 is . Thus, it must be 1, 3, 7, or 15. Moroever, for a non-abelian group, the socle can have order either 2 or 4 (cannot have order 8 or 16) so the number of normal subgroups is either 1 or 3.
- For groups of the same Hall-Senior genus, the number of normal subgroups of a given order are equal. Thus, groups with Hall-Senior symbols and have the same number of normal subgroups of order 4, for instance.
- For an abelian group, the number of subgroups of a given order equals the number of normal subgroups. Moreover, because subgroup lattice and quotient lattice of finite abelian group are isomorphic, we get that (number of subgroups of order 2) = (number of normal subgroups of order 2) = (number of subgroups of order 8) = (number of normal subgroups of order 8), and separately, (number of subgroups of order 4) = (number of normal subgroups of order 4).
| Group | Second part of GAP ID | Hall-Senior number | Hall-Senior symbol | Nilpotency class | number of subgroups of order 2 (must be odd) | number of normal subgroups of order 2 (must be 1, 3, 7, or 15) (by (4)) | number of subgroups of order 4 (must be odd) | number of normal subgroups of order 4 (must be odd) | number of subgroups of order 8 (must be 1, 3, 7, or 15) (see (2) and (3)) | number of normal subgroups of order 8 (must equal preceding column by (2)) |
|---|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 3 | 3 | 7 | 7 | 3 | 3 | |
| SmallGroup(16,3) | 3 | 9 | 2 | 7 | 3 | 11 | 3 | 3 | 3 | |
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 3 | 7 | 3 | 3 | 3 | |
| direct product of Z8 and Z2 | 5 | 4 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | |
| M16 | 6 | 11 | 2 | 3 | 1 | 3 | 3 | 3 | 3 | |
| dihedral group:D16 | 7 | 12 | 3 | 9 | 1 | 5 | 1 | 3 | 3 | |
| semidihedral group:SD16 | 8 | 13 | 3 | 5 | 1 | 5 | 1 | 3 | 3 | |
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 1 | 5 | 1 | 3 | 3 | |
| direct product of Z4 and V4 | 10 | 2 | 1 | 7 | 7 | 11 | 11 | 7 | 7 | |
| direct product of D8 and Z2 | 11 | 6 | 2 | 11 | 3 | 15 | 7 | 7 | 7 | |
| direct product of Q8 and Z2 | 12 | 7 | 2 | 3 | 3 | 7 | 7 | 7 | 7 | |
| central product of D8 and Z4 | 13 | 8 | 2 | 7 | 1 | 7 | 7 | 7 | 7 | |
| elementary abelian group:E16 | 14 | 1 | 1 | 15 | 15 | 35 | 35 | 15 | 15 | |
| Possibility set | -- | -- | -- | 1, 2, 3 | 1, 3, 5, 7, 9, 11, 15 | 1, 3, 7, 15 | 1, 3, 5, 7, 11, 15, 35 | 1, 3, 7, 11, 35 | 1, 3, 7, 15 | 1, 3, 7, 15 |
Subgroups of order 2
The table below provides information on the counts of subgroups of order 2. Note the following:
| General assertion | Implication for the counts in this case |
|---|---|
| congruence condition on number of subgroups of given prime power order | The number of subgroups of order 2 is odd. The number of normal subgroups of order 2 is odd. The number of p-core-automorphism-invariant subgroups (which in this case means the number of subgroups invariant under automorphisms in the 2-core of the automorphism group) is odd. |
| formula for number of minimal normal subgroups of group of prime power order (follows from minimal normal implies contained in Omega-1 of center for nilpotent p-group, which in turn follows from minimal normal implies central in nilpotent, which in turn follows from nilpotent implies center is normality-large). The number of normal subgroups of prime order is thus , where . For a non-abelian group, . | In our case, the number of normal subgroups of order 2 is , which must be one of the numbers 1,3,7,15. For a non-abelian group, the socle cannot have order 16 or 32, so the number of normal subgroups of order 2 is one of the numbers 1 or 3. |
| Group | Second part of GAP ID | Hall-Senior number | Hall-Senior symbol | Nilpotency class | number of subgroups of order 2 (must be odd) | number of normal subgroups of order 2 (must be odd; for a non-abelian group, must be 1 or 3) | number of 2-core-automorphism-invariant subgroups (must be odd; for a non-abelian group, must be 1 or 3) | number of 2-automorphism-invariant subgroups | number of characteristic subgroups |
|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 3 | 3 | ||||
| SmallGroup(16,3) | 3 | 9 | 2 | 7 | 3 | ||||
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 3 | ||||
| direct product of Z8 and Z2 | 5 | 4 | 1 | 3 | 3 | ||||
| M16 | 6 | 11 | 2 | 3 | 1 | ||||
| dihedral group:D16 | 7 | 12 | 3 | 9 | 1 | ||||
| semidihedral group:SD16 | 8 | 13 | 3 | 5 | 1 | ||||
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 1 | ||||
| direct product of Z4 and V4 | 10 | 2 | 1 | 7 | 7 | ||||
| direct product of D8 and Z2 | 11 | 6 | 2 | 11 | 3 | ||||
| direct product of Q8 and Z2 | 12 | 7 | 2 | 3 | 3 | ||||
| central product of D8 and Z4 | 13 | 8 | 2 | 7 | 1 | ||||
| elementary abelian group:E16 | 14 | 1 | 1 | 15 | 15 |
Central series
We have nilpotency class and order determine group up to commutator map-equivalence for up to prime-fourth order. Further/in particular, the nilpotency class and order determines the equivalence class up to isoclinism.
In particular, the isomorphism classes of the successive quotients for the lower central series as well as the isomorphism classes for the successive quotients for the upper central series are determined by the nilpotency class.
With the exception of the whole group, the isomorphism classes of the lower central series members and upper central series members are determined by the Hall-Senior genus.
Below are some of the details that are determined via the Hall-Senior family and genus about the lower and upper central series. Note the following special thing about the order 16 (and more generally, order where is prime and ) -- that the nilpotency class determines the equivalence class up to isoclinism.
Abelian groups
We first consider the abelian groups, i.e., the groups of nilpotency class exactly one. There are five such groups: cyclic group:Z16 (ID: (16,1)), direct product of Z4 and Z4 (ID: (16,2)), direct product of Z8 and Z2 (ID: (16,5)), direct product of Z4 and V4 (ID: (16,10)), and elementary abelian group:E16 (ID: (16,14)). In all these cases, the derived subgroup is trivial (so the lower central series reaches the trivial subgroup in its second step) and the center is the whole group (so the upper central series reaches the whole group at once). Thus, the abelianization is the whole group and the inner automorphism group is trivial.
Groups of class two
These all form a single Hall-Senior family . Note that the third member of the lower central series is trivial, and so is the second member of the upper central series. See below:
| Quantity | Value as abstract group (in general) | Genus | Genus | Genus | Genus |
|---|---|---|---|---|---|
| -- | -- | includes groups direct product of D8 and Z2 (ID: (16,11)) and direct product of Q8 and Z2 (ID: (16,12)) | only the group central product of D8 and Z4 (ID: (16,13)) | includes groups SmallGroup(16,3) (ID: (16,3)) and nontrivial semidirect product of Z4 and Z4 (ID: (16,4)) | only the group M16 (ID: (16,6)) |
| derived subgroup (second member of lower central series) | cyclic group:Z2 | cyclic group:Z2 | cyclic group:Z2 | cyclic group:Z2 | cyclic group:Z2 |
| center (first member of upper central series) | depends on genus | Klein four-group | cyclic group:Z4 | Klein four-group | cyclic group:Z4 |
| abelianization (quotient of whole group by derived subgroup) | depends on genus | elementary abelian group:E8 | elementary abelian group:E8 | direct product of Z4 and Z2 | direct product of Z4 and Z2 |
| inner automorphism group (quotient of whole group by center) | Klein four-group | Klein four-group | Klein four-group | Klein four-group | Klein four-group |
Groups of class three
They all form a single Hall-Senior family and a single Hall-Senior genus . The groups are dihedral group:D16 (ID: (16,7)), semidihedral group:SD16 (ID: (16,8)), generalized quaternion group:Q16 (ID: (16,9)).
All the groups of order 16 and class three are UL-equivalent groups, i.e., the lower and upper central series coincide. In other words, the center is the third member of the lower central series, and the derived subgroup is the second member of the upper central series.
| Quantity | Value as abstract group |
|---|---|
| derived subgroup (second member of lower central series) = second center | cyclic group:Z4 |
| third member of lower central series = center | cyclic group:Z2 |
| abelianization = quotient by derived subgroup | Klein four-group |
| quotient of derived subgroup by third member of lower central series = quotient of second member of upper central series by center | cyclic group:Z2 |
| inner automorphism group = quotient by center = quotient by third member of lower central series | dihedral group:D8 |
Abelian subgroups
Further information: abelian subgroup structure of groups of order 16
Counts of abelian subgroups and abelian normal subgroups
Below is a table with information on the counts of abelian subgroups and abelian normal subgroups in groups of order 16.
- Congruence condition on number of subgroups of given prime power order tells us that for any fixed order, the number of subgroups is congruent to 1 mod 2 (i.e., it is odd). Since the non-normal subgroups occur in conjugacy classes whose size is a nontrivial power of 2, the number of normal subgroups is congruent to 1 mod 2. In particular, for orders 2 and 4, since every subgroup of that order is abelian anyway, the congruence condition tells us that the number of abelian subgroups is congruent to 1 mod 2, and so is the number of abelian normal subgroups.
- Congruence condition on number of abelian subgroups of prime-cube order and existence of abelian normal subgroups of small prime power order: This gives us that the number of abelian subgroups of order 8 is congruent to 1 mod 2 (i.e., it is odd). Hence, the number of abelian normal subgroups of order 8 is also congruent to 1 mod 2 (i.e., it is odd).
The upshot is that all counts in the table below are odd.
- Index two implies normal, so all the abelian subgroups of order 8 are normal. Thus the count for abelian subgroups of order 8 is the same as the count for abelian normal subgroups of order 8.
- For the abelian groups: note that abelian implies every subgroup is normal and also that subgroup lattice and quotient lattice of finite abelian group are isomorphic. Thus, when the whole group is abelian, we have: number of abelian subgroups of order 2 = number of abelian normal subgroups of order 2 = number of abelian subgroups of order 8 = number of abelian normal subgroups of order 8. Separately, we have number of abelian subgroups of order 4 = number of abelian normal subgroups of order 4.
- The "number of abelian normal subgroups" columns depend only on the Hall-Senior genus, i.e., two groups with the same Hall-Senior genus have the same "number of abelian normal subgroups" of each order. The Hall-Senior genus is the part of the Hall-Senior symbol excluding the very final subscript, so for instance and both belong to the Hall-Senior genus .
| Group | GAP ID (2nd part) | Hall-Senior number | Hall-Senior symbol | Nilpotency class | Number of abelian subgroups of order 2 | Number of abelian normal subgroups of order 2 | Number of abelian subgroups of order 4 | Number of abelian normal subgroups of order 4 | Number of abelian subgroups of order 8 | Number of abelian normal subgroups of order 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| cyclic group:Z16 | 1 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| direct product of Z4 and Z4 | 2 | 3 | 1 | 3 | 3 | 7 | 7 | 3 | 3 | |
| SmallGroup(16,3) | 3 | 9 | 2 | 7 | 3 | 11 | 3 | 3 | 3 | |
| nontrivial semidirect product of Z4 and Z4 | 4 | 10 | 2 | 3 | 3 | 7 | 3 | 3 | 3 | |
| direct product of Z8 and Z2 | 5 | 4 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | |
| M16 | 6 | 11 | 2 | 3 | 1 | 3 | 3 | 3 | 3 | |
| dihedral group:D16 | 7 | 12 | 3 | 9 | 1 | 5 | 1 | 1 | 1 | |
| semidihedral group:SD16 | 8 | 13 | 3 | 5 | 1 | 5 | 1 | 1 | 1 | |
| generalized quaternion group:Q16 | 9 | 14 | 3 | 1 | 1 | 5 | 1 | 1 | 1 | |
| direct product of Z4 and V4 | 10 | 2 | 1 | 7 | 7 | 11 | 11 | 7 | 7 | |
| direct product of D8 and Z2 | 11 | 6 | 2 | 11 | 3 | 15 | 7 | 3 | 3 | |
| direct product of Q8 and Z2 | 12 | 7 | 2 | 3 | 3 | 7 | 7 | 3 | 3 | |
| central product of D8 and Z4 | 13 | 8 | 2 | 7 | 1 | 7 | 7 | 3 | 3 | |
| elementary abelian group:E16 | 14 | 1 | 1 | 15 | 15 | 35 | 35 | 15 | 15 |
Counts of abelian characteristic subgroups
Below is information on the counts of abelian characteristic subgroups in groups of order 16.
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]