Groups of order 16

This article gives information about, and links to more details on, groups of order 16
See pages on algebraic structures of order 16| See pages on groups of a particular order

This article gives basic information comparing and contrasting groups of order 16. See also more detailed information on specific subtopics through the links:

Information type	Page summarizing information for groups of order 16
element structure (element orders, conjugacy classes, etc.)	element structure of groups of order 16
subgroup structure	subgroup structure of groups of order 16
linear representation theory	linear representation theory of groups of order 16 projective representation theory of groups of order 16 modular representation theory of groups of order 16
endomorphism structure, automorphism structure	endomorphism structure of groups of order 16
group cohomology	group cohomology of groups of order 16

Statistics at a glance

To understand these in a broader context, see
groups of order 2^n |groups of prime-fourth order

Numbers of groups

Quantity	Value	Explanation
Total number of groups	14
Number of abelian groups	5	equals the number of unordered integer partitions of 4. See classification of finite abelian groups and structure theorem for finitely generated abelian groups.
Number of non-abelian groups of class two	6
Number of groups of nilpotency class exactly three, i.e., maximal class groups	3	classification of finite 2-groups of maximal class. For order $2^n, n \ge 4$, there are exactly three maximal class groups: dihedral, semidihedral, and generalized quaternion. For order 16, the groups are: dihedral group:D16, semidihedral group:SD16, and generalized quaternion group:Q16.

Numbers of equivalence classes of groups

Equivalence relation on groups	Number of equivalence classes of groups of order 16	Sizes of equivalence classes, i.e., number of isomorphism classes of groups within each equivalence class (should add up to 14)	More information
isoclinic groups (i.e., Hall-Senior families)	3	5,6,3	#Families and classification, see also classification of groups of order 16. For order 16, the nilpotency class is sufficient to determine the group up to isoclinism.
having the same conjugacy class size statistics	3	5,6,3	Element structure of groups of order 16#Conjugacy class sizes. For order 16, as for other small prime power orders, the nilpotency class determines the conjugacy class size statistics, and vice versa. See nilpotency class and order determine conjugacy class size statistics for groups up to prime-fourth order.
having the same degrees of irreducible representations	3	5,6,3	See Linear representation theory of groups of order 16#Degrees of irreducible representations. Note that for order 16, as for other small prime power orders, the nilpotency class determines the conjugacy class size statistics, and vice versa. See nilpotency class and order determine conjugacy class size statistics for groups up to prime-fourth order.
1-isomorphic groups	12	1 (10 times), 2 (2 times)	Element structure of groups of order 16#1-isomorphism

The list

IDs and symbols

Group	Second part of GAP ID (GAP ID is (16,second part))	Hall-Senior number (among groups of order 16)	Nilpotency class	Hall-Senior symbol	Probability in cohomology tree probability distribution (as proper fraction)	Probability in cohomology tree probability distribution (as numerical value)
cyclic group:Z16	1	5	1	$(4)$	1/8	0.1250
direct product of Z4 and Z4	2	3	1	$(2^2)$	7/128	0.0547
SmallGroup(16,3)	3	9	2	$16\Gamma_2c_1$	13/128	0.1016
nontrivial semidirect product of Z4 and Z4	4	10	2	$16\Gamma_2c_2$	1/8	0.1250
direct product of Z8 and Z2	5	4	1	$(31)$	15/64	0.2344
M16	6	11	2	$16\Gamma_2d$	7/64	0.1094
dihedral group:D16	7	12	3	$16\Gamma_3a_1$	3/128	0.0234
semidihedral group:SD16	8	13	3	$16\Gamma_3a_2$	3/64	0.0469
generalized quaternion group:Q16	9	14	3	$16\Gamma_3a_3$	3/128	0.0234
direct product of Z4 and V4	10	2	1	$(21^2)$	63/1024	0.0615
direct product of D8 and Z2	11	6	2	$16\Gamma_2a_1$	45/1024	0.0440
direct product of Q8 and Z2	12	7	2	$16\Gamma_2a_2$	23/1024	0.0225
central product of D8 and Z4	13	8	2	$16\Gamma_2b$	7/256	0.0273
elementary abelian group:E16	14	1	1	$(1^4)$	1/1024	0.0010

Presentations

In these presentations, we use $e$ for the identity element.

Group	Second part of GAP ID (GAP ID is (16,second part))	Hall-Senior number (among groups of order 16)	Presentation
cyclic group:Z16	1	5	$\langle a \mid a^{16} = e \rangle$
direct product of Z4 and Z4	2	3	$\langle a,b \mid a^4 = b^4 = e, ab = ba \rangle$
SmallGroup(16,3)	3	9	$\langle a,b,c \mid a^4 = b^2 = c^2 = e, ab = ba, bc = cb, cac^{-1} = ab \rangle$
nontrivial semidirect product of Z4 and Z4	4	10	$\langle a,b \mid a^4 = b^4 = e, bab^{-1} = a^3 \rangle$
direct product of Z8 and Z2	5	4	$\langle a,b \mid a^8 = b^2 = e, ab = ba \rangle$
M16	6	11	$\langle a,x \mid a^8 = x^2 = e, xax^{-1} = a^5 \rangle$
dihedral group:D16	7	12	$\langle a,x \mid a^8 = x^2 = e, xax^{-1} = a^{-1} \rangle$
semidihedral group:SD16	8	13	$\langle a,x \mid a^8 = x^2 = e, xax^{-1} = a^3 \rangle$
generalized quaternion group:Q16	9	14	$\langle a,b \mid a^4 = b^2 = abab\rangle$
direct product of Z4 and V4	10	2	$\langle a,b,c \mid a^4 = b^2 = c^2 = e, ab = ba, bc = cb, ac = ca \rangle$
direct product of D8 and Z2	11	6	$\langle a,x,y \mid a^4 = x^2 = y^2 = e, xax^{-1} = a^{-1}, ay = ya, xy = yx \rangle$
direct product of Q8 and Z2	12	7	$\langle a,b,c \mid a^2 = b^2 = abab, c^2 = e, ac = ca, bc = cb \rangle$ (check)
central product of D8 and Z4	13	8	$\langle a,x,y \mid a^4 = x^2 = e, a^2 = y^2, xax^{-1} = a^{-1}, xy = yx, ay = ya \rangle$
elementary abelian group:E16	14	1	$\langle a,b,c,d \mid a^2 = b^2 = c^2 = d^2 = e, ab = ba, ac = ca, bc = cb, ad = da, bd = db, cd = dc \rangle$

Permutation representations

These give faithful permutation representations of the group:

Group	Second part of GAP ID (GAP ID is (16,second part))	Hall-Senior number (among groups of order 16)	Permutation representation
cyclic group:Z16	1	5	$\langle (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16) \rangle$
direct product of Z4 and Z4	2	3	$\langle (1,2,3,4), (5,6,7,8) \rangle$
SmallGroup(16,3)	3	9	$\langle (1,2,3,4),(1,3)(5,6,7,8) \rangle$
nontrivial semidirect product of Z4 and Z4	4	10	$\langle (1,2,3,4), (1,3)(5,6,7,8)\rangle$
direct product of Z8 and Z2	5	4	$\langle (1,2,3,4,5,6,7,8), (9,10) \rangle$
M16	6	11	$\langle (1,2,3,4,5,6,7,8), (1,5)(3,7) \rangle$
dihedral group:D16	7	12	$\langle (1,2,3,4,5,6,7,8), (1,7)(3,5)(2,6) \rangle$
semidihedral group:SD16	8	13	$\langle (1,2,3,4,5,6,7,8), (1,3)(5,7)(2,6) \rangle$
generalized quaternion group:Q16	9	14	$\langle (1,2,3,4,5,6,7,8)(9,10,11,12,13,14,15,16),(1,9,5,13)(2,16,6,12)(3,15,7,11)(4,14,8,10) \rangle$
direct product of Z4 and V4	10	2	$\langle (1,2,3,4), (5,6), (7,8)\rangle$
direct product of D8 and Z2	11	6	$\langle (1,2,3,4), (1,3), (5,6)\rangle$
direct product of Q8 and Z2	12	7	$\langle (1,2,4,7)(3,6,8,5),(1,3,4,8)(2,5,7,6),(9,10) \rangle$
central product of D8 and Z4	13	8	$\langle (1,2,3,4)(5,6,7,8),(1,7)(2,8)(3,5)(4,6),(1,6,3,8)(2,5,4,7) \rangle$
elementary abelian group:E16	14	1	$\langle (1,2), (3,4), (5,6), (7,8)\rangle$

Here is the GAP code verifying that these permutation representations work: [SHOW MORE]

gap> IdGroup(Group([(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)]));
[ 16, 1 ]
gap> IdGroup(Group([(1,2,3,4),(5,6,7,8)]));
[ 16, 2 ]
gap> IdGroup(Group([(1,2)(3,4),(1,3)(2,4),(1,3)(5,6,7,8)]));                                                                                                             
[ 16, 3 ]
gap> IdGroup(Group([(1,2,3,4),(1,3)(5,6,7,8)]));
[ 16, 4 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(9,10)]));
[ 16, 5 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,5)(3,7)]));
[ 16, 6 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,7)(3,5)(2,6)]));
[ 16, 7 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,3)(5,7)(2,6)]));
[ 16, 8 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8)(9,10,11,12,13,14,15,16),(1,9,5,13)(2,16,6,12)(3,15,7,11)(4,14,8,10)]));                                                            
[ 16, 9 ]
gap> IdGroup(Group([(1,2,3,4),(5,6),(7,8)]));
[ 16, 10 ]
gap> IdGroup(Group([(1,2,3,4),(1,3),(5,6)]));
[ 16, 11 ]
gap> IdGroup(Group([(1,2,4,7)(3,6,8,5),(1,3,4,8)(2,5,7,6),(9,10)]));
[ 16, 12 ]
gap> IdGroup(Group([(1,2,3,4)(5,6,7,8),(1,7)(2,8)(3,5)(4,6),(1,6,3,8)(2,5,4,7)]));                                                                                    
[ 16, 13 ]
gap> IdGroup(Group([(1,2),(3,4),(5,6),(7,8)]));
[ 16, 14 ]

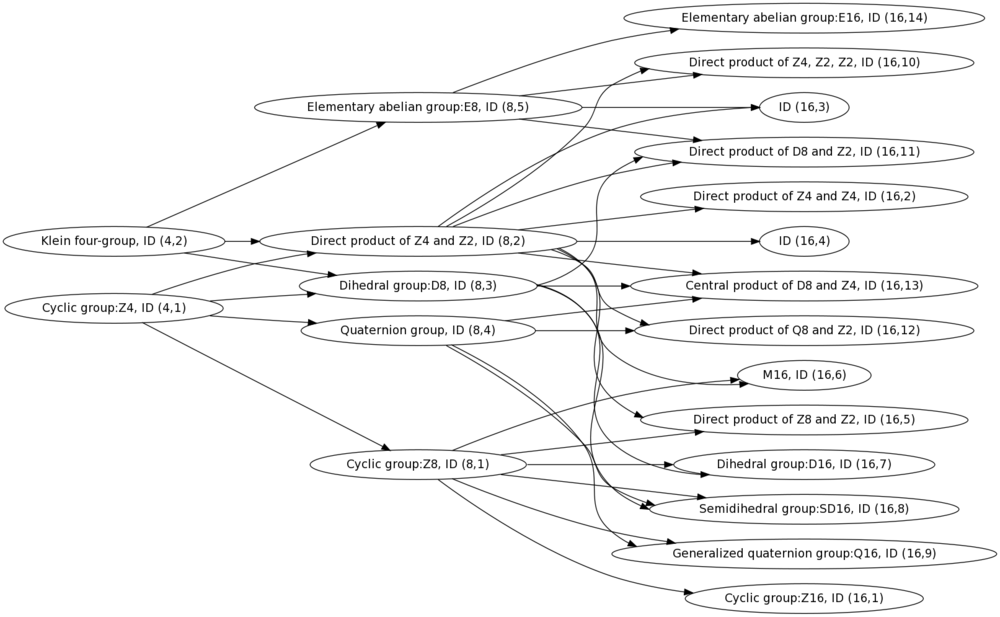
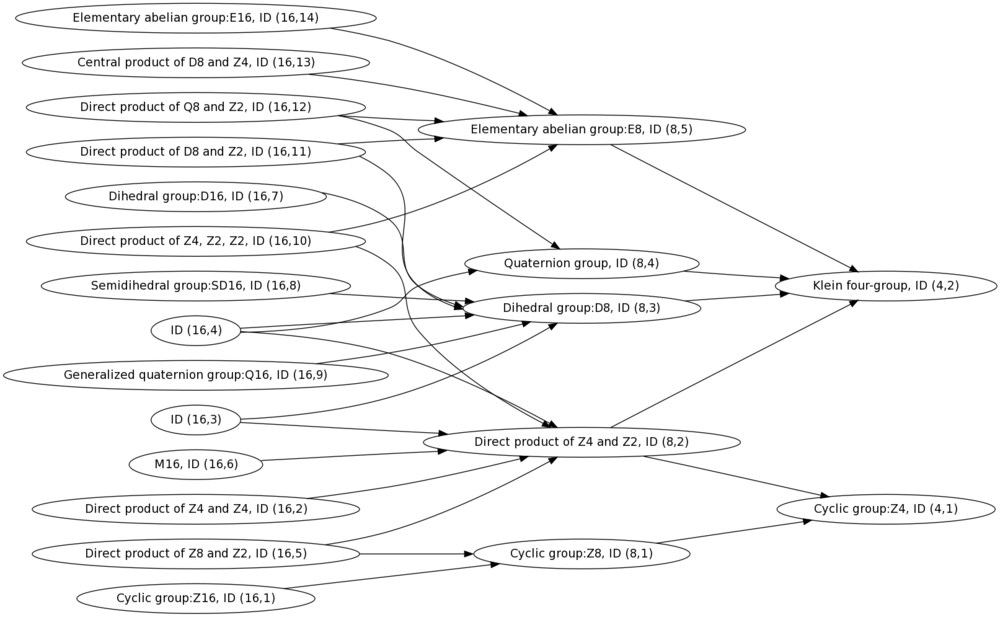
Subgroup/quotient relationships

Subgroup relationships

Quotient relationships

Arithmetic functions

Summary information

Here, the rows are arithmetic functions that take values between $0$ and $4$, and the columns give the possible values of these functions. The entry in each cell is the number of isomorphism classes of groups for which the row arithmetic function takes the column value. Note that all the row value sums must equal $14$.

Arithmetic function	Value 0	Value 1	Value 2	Value 3	Value 4
prime-base logarithm of exponent	0	1	7	5	1
nilpotency class	0	5	6	3	0
derived length	0	5	9	0	0
Frattini length	0	1	7	5	1
minimum size of generating set	0	1	8	4	1
number of factors in direct product decomposition	0	8	4	1	1

Functions taking values between 0 and 4

These measure ranks of subgroups, lengths of series, or the prime-base logarithms of orders of certain subgroups.

Group	GAP ID second part	Hall-Senior number	prime-base logarithm of exponent	nilpotency class	derived length	Frattini length	minimum size of generating set	subgroup rank	rank	normal rank	characteristic rank	prime-base logarithm of order of derived subgroup	prime-base logarithm of order of inner automorphism group	number of factors in complete direct product decomposition
cyclic group:Z16	1	5	4	1	1	4	1	1	1	1	1	0	0	1
direct product of Z4 and Z4	2	3	2	1	1	2	2	2	2	2	2	0	0	2
SmallGroup(16,3)	3	9	2	2	2	2	2	3	3	3	3	1	2	1
nontrivial semidirect product of Z4 and Z4	4	10	2	2	2	2	2	2	2	2	2	1	2	1
direct product of Z8 and Z2	5	4	3	1	1	3	2	2	2	2	2	0	0	2
M16	6	11	3	2	2	3	2	2	2	2	2	1	2	1
dihedral group:D16	7	12	3	3	2	3	2	2	2	1	1	2	3	1
semidihedral group:SD16	8	13	3	3	2	3	2	2	2	1	1	2	3	1
generalized quaternion group:Q16	9	14	3	3	2	3	2	2	1	1	1	2	3	1
direct product of Z4 and V4	10	2	2	1	1	2	3	3	3	3	3	0	0	3
direct product of D8 and Z2	11	6	2	2	2	2	3	3	3	3	2	1	2	2
direct product of Q8 and Z2	12	7	2	2	2	2	3	3	2	2	2	1	2	2
central product of D8 and Z4	13	8	2	2	2	2	3	3	2	2	1	1	2	1
elementary abelian group:E16	14	1	1	1	1	1	4	4	4	4	4	0	0	4

Here now is the same table along with various measures of averages and deviations:[SHOW MORE]

Group	GAP ID second part	Hall-Senior number	prime-base logarithm of exponent	nilpotency class	derived length	Frattini length	minimum size of generating set	subgroup rank	rank	normal rank	characteristic rank	prime-base logarithm of order of derived subgroup	prime-base logarithm of order of inner automorphism group
cyclic group:Z16	1	5	4	1	1	4	1	1	1	1	1	0	0
direct product of Z4 and Z4	2	3	2	1	1	2	2	2	2	2	2	0	0
SmallGroup(16,3)	3	9	2	2	2	2	2	3	3	3	3	1	2
nontrivial semidirect product of Z4 and Z4	4	10	2	2	2	2	2	2	2	2	2	1	2
direct product of Z8 and Z2	5	4	3	1	1	3	2	2	2	2	2	0	0
M16	6	11	3	2	2	3	2	2	2	2	2	1	2
dihedral group:D16	7	12	3	3	2	3	2	2	2	1	1	2	3
semidihedral group:SD16	8	13	3	3	2	3	2	2	2	1	1	2	3
quaternion group	9	14	3	3	2	3	2	2	1	1	1	2	3
direct product of Z4 and V4	10	2	2	1	1	2	3	3	3	3	3	0	0
direct product of D8 and Z2	11	6	2	2	2	2	3	3	3	3	2	1	2
direct product of Q8 and Z2	12	7	2	2	2	2	3	3	2	2	2	1	2
central product of D8 and Z4	13	8	2	2	2	2	3	3	2	2	1	1	2
elementary abelian group:E16	14	1	1	1	1	1	4	4	4	4	4	0	0
Total			34	26	23	34	33	34	31	29	27	12	21
Mean			2.43	1.86	1.64	2.43	2.36	2.43	2.21	2.07	1.93	0.86	1.5
Median			2	2	2	2	2	2	2	2	2	1	2
Mode			2	2	2	2	2	2	2	2	2	1	2
Standard deviation			0.76	0.77	0.5	0.76	0.74	0.76	0.8	0.92	0.92	0.77	1.22
Standard deviation to mean ratio			0.31	0.41	0.3	0.31	0.32	0.31	0.36	0.44	0.48	0.9	0.82

Same, with rows and columns interchanged:

Function	1	2	3	4	5	6	7	8	9	10	11	12	13	14
prime-base logarithm of exponent	4	2	2	2	3	3	3	3	3	2	2	2	2	1
nilpotency class	1	1	2	2	1	2	3	3	3	1	2	2	2	1
derived length	1	1	2	2	1	2	2	2	2	1	2	2	2	1
Frattini length	4	2	2	2	3	3	3	3	3	2	2	2	2	1
minimum size of generating set	1	2	2	2	2	2	2	2	2	3	3	3	3	4
subgroup rank	1	2	3	2	2	2	2	2	2	3	3	3	3	4
rank as p-group	1	2	3	2	2	2	2	2	1	3	3	2	2	4
normal rank as p-group	1	2	3	2	2	2	1	1	1	3	3	2	2	4
characteristic rank as p-group	1	2	3	2	2	2	1	1	1	3	2	2	1	4
prime-base logarithm of order of derived subgroup	0	0	1	1	0	1	2	2	2	0	1	1	1	0
prime-base logarithm of order of inner automorphism group	0	0	2	2	0	2	3	3	3	0	2	2	2	0

Here are the correlations between these various arithmetic functions across the groups of order 16: [SHOW MORE]

Arithmetic function	prime-base logarithm of exponent	nilpotency class	derived length	Frattini length	minimum size of generating set	subgroup rank	rank	normal rank	characteristic rank	prime-base logarithm of order of derived subgroup	prime-base logarithm of order of inner automorphism group
prime-base logarithm of exponent	1	0.25	0.03	1	-0.84	-0.88	-0.8	-0.82	-0.73	0.25	0.17
nilpotency class	0.25	1	0.86	0.25	-0.17	-0.15	-0.32	-0.53	-0.56	1	0.98
derived length	0.03	0.86	1	0.03	-0.04	0.03	-0.18	-0.28	-0.4	0.86	0.95
Frattini length	1	0.25	0.03	1	-0.84	-0.88	-0.8	-0.82	-0.73	0.25	0.17
minimum size of generating set	-0.84	-0.17	-0.04	-0.84	1	0.94	0.76	0.75	0.6	-0.17	-0.13
subgroup rank	-0.88	-0.15	0.03	-0.88	0.94	1	0.85	0.84	0.71	-0.15	-0.08
rank as p-group	-0.8	-0.32	-0.18	-0.8	0.76	0.85	1	0.92	0.86	-0.32	-0.27
normal rank as p-group	-0.82	-0.53	-0.28	-0.82	0.75	0.84	0.92	1	0.92	-0.53	-0.45
characteristic rank as p-group	-0.73	-0.56	-0.4	-0.73	0.6	0.71	0.86	0.92	1	-0.56	-0.51
prime-base logarithm of order of derived subgroup	0.25	1	0.86	0.25	-0.17	-0.15	-0.32	-0.53	-0.56	1	0.98
prime-base logarithm of order of inner automorphism group	0.17	0.98	0.95	0.17	-0.13	-0.08	-0.27	-0.45	-0.51	0.98	1

Arithmetic function values of a counting nature

Group	GAP ID second part	Hall-Senior number	number of conjugacy classes	number of subgroups	number of conjugacy classes of subgroups	number of normal subgroups	number of characteristic subgroups	number of automorphism classes of subgroups
cyclic group:Z16	1	5	16	5	5	5	5	5
direct product of Z4 and Z4	2	3	16	15	15	15	3
SmallGroup(16,3)	3	9	10	23	17	11	5
nontrivial semidirect product of Z4 and Z4	4	10	10	15	13	11	7
direct product of Z8 and Z2	5	4	16	11	11	11	7
M16	6	11	10	11	10	9	7
dihedral group:D16	7	12	7	19	11	7	5	9
semidihedral group:SD16	8	13	7	15	10	7	7
quaternion group	9	14	7	11	9	7	5
direct product of Z4 and V4	10	2	16	27	27	27	4
direct product of D8 and Z2	11	6	10	35	27	19	5
direct product of Q8 and Z2	12	7	10	19	19	19	4
central product of D8 and Z4	13	8	10	23	20	17	5
elementary abelian group:E16	14	1	16	67	67	67	2	5

Here are the GAP commands/code for these: [SHOW MORE]

For everything except automorphism classes of subgroups, the following code works. Note that you may need to load the Sonata package to access the Subgroups function.

gap> F := List(AllSmallGroups(16),G -> List([ConjugacyClasses(G),Subgroups(G),ConjugacyClassesSubgroups(G),
> NormalSubgroups(G),CharacteristicSubgroups(G)],Length));;
gap> K := List([1..14],i -> [i,F[i]]);

GAP's output is:

[ [ 1, [ 16, 5, 5, 5, 5 ] ], [ 2, [ 16, 15, 15, 15, 3 ] ], [ 3, [ 10, 23, 17, 11, 5 ] ], [ 4, [ 10, 15, 13, 11, 7 ] ], [ 5, [ 16, 11, 11, 11, 7 ] ],
  [ 6, [ 10, 11, 10, 9, 7 ] ], [ 7, [ 7, 19, 11, 7, 5 ] ], [ 8, [ 7, 15, 10, 7, 7 ] ], [ 9, [ 7, 11, 9, 7, 5 ] ], [ 10, [ 16, 27, 27, 27, 4 ] ],
  [ 11, [ 10, 35, 27, 19, 5 ] ], [ 12, [ 10, 19, 19, 19, 4 ] ], [ 13, [ 10, 23, 20, 17, 5 ] ], [ 14, [ 16, 67, 67, 67, 2 ] ] ]

Same, with rows and columns interchanged:

Function	1	2	3	4	5	6	7	8	9	10	11	12	13	14
number of conjugacy classes	16	16	10	10	16	10	7	7	7	16	10	10	10	16
number of subgroups	5	15	23	15	11	11	19	15	11	27	35	19	23	67
number of conjugacy classes of subgroups	5	15	17	13	11	10	11	10	9	27	27	19	20	67
number of characteristic subgroups	5	3	5	7	7	7	5	7	5	4	5	4	5	2

Numerical invariants

Here first is the table with the number of conjugacy classes of each size (for more detailed breakdown information, see element structure of groups of order 16). Note also that nilpotency class and order determine conjugacy class size statistics for groups up to prime-fourth order, so that there are only three types -- the abelian groups, the non-abelian groups of class two, and the groups of class exactly three:

Group	GAP ID	Nilpotency class	Conjugacy classes of size 1	Conjugacy classes of size 2	Conjugacy classes of size 4
cyclic group:Z16	1	1	16	0	0
direct product of Z4 and Z4	2	1	16	0	0
SmallGroup(16,3)	3	2	4	6	0
nontrivial semidirect product of Z4 and Z4	4	2	4	6	0
direct product of Z8 and Z2	5	1	16	0	0
M16	6	2	4	6	0
dihedral group:D16	7	3	2	3	2
semidihedral group:SD16	8	3	2	3	2
generalized quaternion group:Q16	9	3	2	3	2
direct product of Z4 and V4	10	1	16	0	0
direct product of D8 and Z2	11	2	4	6	0
direct product of Q8 and Z2	12	2	4	6	0
central product of D8 and Z4	13	2	4	6	0
elementary abelian group:E16	14	1	16	0	0

Here are the degrees of irreducible representations. Note also that nilpotency class and order determine degrees of irreducible representations for groups up to prime-fourth order, so that there are only three types -- the abelian groups, the non-abelian groups of class two, and the groups of class exactly three:

Group	GAP ID	Nilpotency class	Degree 1	Degree 2	Degree 4
cyclic group:Z16	1	1	16	0	0
direct product of Z4 and Z4	2	1	16	0	0
SmallGroup(16,3)	3	2	8	2	0
nontrivial semidirect product of Z4 and Z4	4	2	8	2	0
direct product of Z8 and Z2	5	1	16	0	0
M16	6	2	8	2	0
dihedral group:D16	7	3	4	3	0
semidihedral group:SD16	8	3	4	3	0
generalized quaternion group:Q16	9	3	4	3	0
direct product of Z4 and V4	10	1	16	0	0
direct product of D8 and Z2	11	2	8	2	0
direct product of Q8 and Z2	12	2	8	2	0
central product of D8 and Z4	13	2	8	2	0
elementary abelian group:E16	14	1	16	0	0

Here is the lower central series information. Again, notice that the nilpotency class determines the information. Further information: nilpotency class and order determine orders of lower central series members for groups up to prime-fourth order

Group	GAP ID	Nilpotency class	Prime-base logarithm of first lower central series quotient	Prime-base logarithm of second lower central series quotient	Prime-base logarithm of third lower central series quotient
cyclic group:Z16	1	1	4	0	0
direct product of Z4 and Z4	2	1	4	0	0
SmallGroup(16,3)	3	2	3	1	0
nontrivial semidirect product of Z4 and Z4	4	2	3	1	0
direct product of Z8 and Z2	5	1	4	0	0
M16	6	2	3	1	0
dihedral group:D16	7	3	2	1	1
semidihedral group:SD16	8	3	2	1	1
generalized quaternion group:Q16	9	3	2	1	1
direct product of Z4 and V4	10	1	4	0	0
direct product of D8 and Z2	11	2	3	1	0
direct product of Q8 and Z2	12	2	3	1	0
central product of D8 and Z4	13	2	3	1	0
elementary abelian group:E16	14	1	4	0	0

Here is the upper central series information. Again, notice that the nilpotency class determines the information. Further information: nilpotency class and order determine orders of upper central series members for groups up to prime-fourth order

Group	GAP ID	Nilpotency class	Prime-base logarithm of first upper central series quotient	Prime-base logarithm of second upper central series quotient	Prime-base logarithm of third upper central series quotient
cyclic group:Z16	1	1	4	0	0
direct product of Z4 and Z4	2	1	4	0	0
SmallGroup(16,3)	3	2	2	2	0
nontrivial semidirect product of Z4 and Z4	4	2	2	2	0
direct product of Z8 and Z2	5	1	4	0	0
M16	6	2	2	2	0
dihedral group:D16	7	3	1	1	2
semidihedral group:SD16	8	3	1	1	2
generalized quaternion group:Q16	9	3	1	1	2
direct product of Z4 and V4	10	1	4	0	0
direct product of D8 and Z2	11	2	2	2	0
direct product of Q8 and Z2	12	2	2	2	0
central product of D8 and Z4	13	2	2	2	0
elementary abelian group:E16	14	1	4	0	0

Group properties

Basic properties

The column headings represent the IDs of the groups:

Property	1	2	3	4	5	6	7	8	9	10	11	12	13	14
cyclic group	Yes	No	No	No	No	No	No	No	No	No	No	No	No	No
elementary abelian group	No	No	No	No	No	No	No	No	No	No	No	No	No	Yes
homocyclic group	Yes	Yes	No	No	No	No	No	No	No	No	No	No	No	Yes
metacyclic group	Yes	Yes	No	No	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No
abelian group	Yes	Yes	No	No	Yes	No	No	No	No	Yes	No	No	No	Yes

Properties related to conjugacy classes/representations

Property	1	2	3	4	5	6	7	8	9	10	11	12	13	14
ambivalent group	No	No	No	No	No	No	Yes	No	Yes	No	Yes	Yes	No	Yes
rational group	No	No	No	No	No	No	No	No	No	No	Yes	Yes	No	Yes
rational-representation group	No	No	No	No	No	No	No	No	No	No	Yes	No	No	Yes
group in which every element is automorphic to its inverse	Yes	Yes	?	?	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

Properties related to automorphisms and conjugacy

Property	1	2	3	4	5	6	7	8	9	10	11	12	13	14
group in which every element is automorphic to its inverse	Yes	Yes	?	?	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
group in which any two elements generating the same cyclic subgroup are automorphic	Yes	Yes	?	?	Yes	?	Yes	Yes	Yes	Yes	Yes	Yes	?	Yes
group of prime power order in which all maximal subgroups are isomorphic	Yes	Yes	No	Yes	No	No	No	No	No	No	No	No	No	Yes
group of prime power order in which all maximal subgroups are automorphic	Yes	Yes	No	Yes	No	No	No	No	No	No	No	No	No	Yes
group of prime power order in which every maximal subgroup is isomorph-free	Yes	No	No	No	No	No	No	Yes	No	No	No	No	No	No
UL-equivalent group	Yes	Yes	No	No	Yes	No	Yes	Yes	Yes	Yes	No	No	No	Yes

Families and classification

Up to isoclinism

FACTS TO CHECK AGAINST for isoclinic groups (groups with an isoclinism between them):
by definition, isoclinic groups have isomorphic inner automorphism groups and isomorphic derived subgroups, with the isomorphisms compatible.
isoclinic groups have same nilpotency class|isoclinic groups have same derived length | isoclinic groups have same proportions of conjugacy class sizes | isoclinic groups have same proportions of degrees of irreducible representations

The equivalence classes up to being isoclinic were classified by Hall and Senior, and we call them Hall-Senior families.

Family name	Isomorphism class of inner automorphism group	Isomorphism class of derived subgroup	Number of groups	Nilpotency class	Members	Second part of GAP ID of members (sorted ascending)	Hall-Senior numbers of members (sorted ascending)	Smallest order of group isoclinic to these groups	Stem groups (groups of smallest order)
$\Gamma_1$	trivial group	trivial group	5	1	cyclic group:Z16, direct product of Z4 and Z4, direct product of Z8 and Z2, direct product of Z4 and V4, elementary abelian group:E16	1, 2, 5, 10, 14	1, 2, 3, 4, 5	1	trivial group
$\Gamma_2$	Klein four-group	cyclic group:Z2	6	2	SmallGroup(16,3), nontrivial semidirect product of Z4 and Z4, M16, direct product of D8 and Z2, direct product of Q8 and Z2, central product of D8 and Z4	3, 4, 6, 11, 12, 13	6, 7, 8, 9, 10, 11	8	dihedral group:D8, quaternion group
$\Gamma_3$	dihedral group:D8	cyclic group:Z4	3	3	all maximal class groups: dihedral group:D16, semidihedral group:SD16, generalized quaternion group:Q16	7, 8, 9	12, 13, 14	16	dihedral group:D16, semidihedral group:SD16, generalized quaternion group:Q16
Total (3 rows)	--	--	14	--	--	--	--	--	--

Up to Hall-Senior genus

Two groups have the same Hall-Senior genus if they are isoclinic and their lattice of normal subgroups are isomorphic to each other.

Genus name	Members	Second part of GAP ID of members	Hall-Senior numbers of members
$(1^4)$	elementary abelian group:E16	14	1
$(21^2)$	direct product of Z4 and V4	10	2
$(2^2)$	direct product of Z4 and Z4	2	3
$(31)$	direct product of Z8 and Z2	5	4
$(4)$	cyclic group:Z16	1	5
$16\Gamma_2a$	direct product of D8 and Z2, direct product of Q8 and Z2	11, 12	6, 7
$16\Gamma_2b$	central product of D8 and Z4	13	8
$16\Gamma_2c$	SmallGroup(16,3), nontrivial semidirect product of Z4 and Z4	3, 4	9, 10
$16\Gamma_2d$	M16	6	11
$16\Gamma_3a$	dihedral group:D16, semidihedral group:SD16, generalized quaternion group:Q16	7, 8, 9	12, 13, 14

Up to isologism for class two

Under the equivalence relation of being isologic groups with respect to the variety of groups of nilpotency class two, there are two equivalence classes:

Isomorphism class of quotient by second center	Isomorphism class of third member of lower central series	Number of groups	Nilpotency class(es)	Second part of GAP ID of members (sorted ascending)	Hall-Senior numbers of members (sorted ascending)	Smallest order of group isologic to these groups	Stem groups (groups of smallest order)
trivial group	trivial group	11	1,2	1,2,3,4,5,6,10,11,12,13,14	1-11	1	trivial group
Klein four-group	cyclic group:Z2	3	3	7,8,9	12-14	16	dihedral group:D16, semidihedral group:SD16, generalized quaternion group:Q16

Up to isologism for higher class

For any class equal to three or higher, there is a single equivalence class under isologism for that class for groups of order 16, because all groups of order 16 have class at most three and are hence isologic to the trivial group.

Element structure

Further information: element structure of groups of order 16

1-isomorphism

Further information: element structure of groups of order 16#1-isomorphism

There are two pairs of 1-isomorphic groups: M16 (ID: 6) and direct product of Z8 and Z2 (ID: 5) are 1-isomorphic to each other, and central product of D8 and Z4 (ID: 13)and direct product of Z4 and V4 (ID: 10) are 1-isomorphic to each other.

Order statistics

Further information: element structure of groups of order 16#Order statistics

There are many pairs of order statistics-equivalent groups. In addition to the 1-isomorphic pairs, we also have that direct product of Q8 and Z2 (ID: 12) and nontrivial semidirect product of Z4 and Z4 (ID:4) have the same order statistics as direct product of Z4 and Z4 (ID: 2). Also, the group SmallGroup(16,3) (ID: 3)is order statistics-equivalent to direct product of Z4 and V4, but not 1-isomorphic to it.

Conjugacy class structure

Further information: element structure of groups of order 16#Conjugacy class-cum-order statistics

The sizes of conjugacy classes are completely determined by the nilpotency class of the group. Class 1 (abelian) means that all conjugacy classes are of size 1. Class exactly two means that there are four conjugacy classes of size 1 and six conjugacy classes of size 2. Class exactly three means two conjugacy classes of size 1, three of size 2, and two of size 4.

Linear representation theory

Further information: linear representation theory of groups of order 16

Cohomology: piecing together from groups of smaller orders

Central extensions with abelian groups both sides

We list here those groups arising as extensions with base group $A$ abelian, quotient group also abelian, and the action trivial.

Base group	Extension group	Second cohomology group isomorphism class	Groups obtained as extensions	GAP IDs second part	More information
cyclic group:Z8	cyclic group:Z2	cyclic group:Z2	cyclic group:Z16 (1) and direct product of Z8 and Z2 (1)	1,5	second cohomology group for trivial group action of Z2 on Z8, also supergroups of cyclic group:Z8
cyclic group:Z4	cyclic group:Z4	cyclic group:Z4	direct product of Z4 and Z4 (1), cyclic group:Z16 (2), direct product of Z8 and Z2 (1)	2,1,5	second cohomology group for trivial group action of Z4 on Z4
cyclic group:Z4	Klein four-group	elementary abelian group:E8	direct product of Z4 and V4 (1), direct product of Z8 and Z2 (3), M16 (3), central product of D8 and Z4	10,5,6,13	second cohomology group for trivial group action of V4 on Z4
Klein four-group	Klein four-group	elementary abelian group:E64	elementary abelian group:E16 (1), direct product of Z4 and Z4 (6), direct product of Z4 and V4 (9), SmallGroup(16,3) (18), nontrivial semidirect product of Z4 and Z4 (18), direct product of D8 and Z2 (9), direct product of Q8 and Z2 (3)	14,2,10,3,4,11,12	second cohomology group for trivial group action of V4 on V4

Automorphism groups

Group	GAP ID (second part)	Order of automorphism group	Iso. class of automorphism group	Log_2 of largest power of 2 dividing automorphism group	Iso. class of 2-Sylow subgroup of automorphism group	Log_2 of order of 2-core	Iso. class of 2-core	Log_2 of order of inner automorphism group	Iso. class of inner automorphism group
cyclic group:Z16	1	8	direct product of Z4 and Z2	3	direct product of Z4 and Z2	3	direct product of Z4 and Z2	0	trivial group
direct product of Z4 and Z4	2	96	general linear group:GL(2,Z4)	5	SmallGroup(32,27)	4	elementary abelian group:E16	0	trivial group
SmallGroup(16,3)	3	32	SmallGroup(32,27)	5	SmallGroup(32,27)	5	SmallGroup(32,27)	2	Klein four-group
nontrivial semidirect product of Z4 and Z4	4	32	SmallGroup(32,27)	5	SmallGroup(32,27)	5	SmallGroup(32,27)	2	Klein four-group
direct product of Z8 and Z2	5	16	direct product of D8 and Z2	4	direct product of D8 and Z2	4	direct product of D8 and Z2	0	trivial group
M16	6	16	direct product of D8 and Z2	4	direct product of D8 and Z2	4	direct product of D8 and Z2	2	Klein four-group
dihedral group:D16	7	32	holomorph of Z8	5	holomorph of Z8	5	holomorph of Z8	3	dihedral group:D8
semidihedral group:SD16	8	16	direct product of D8 and Z2	4	direct product of D8 and Z2	4	direct product of D8 and Z2	3	dihedral group:D8
generalized quaternion group:Q16	9	32	holomorph of Z8	5	holomorph of Z8	5	holomorph of Z8	3	dihedral group:D8
direct product of Z4 and V4	10	192	SmallGroup(192,1493)	6	Upper-triangular unipotent matrix group:U(4,2)	5	inner holomorph of D8 (one of the extraspecial groups of order 32)	0	trivial group
direct product of D8 and Z2	11	64	Upper-triangular unipotent matrix group:U(4,2)	6	Upper-triangular unipotent matrix group:U(4,2)	6	Upper-triangular unipotent matrix group:U(4,2)	2	Klein four-group
direct product of Q8 and Z2	12	192	SmallGroup(192,955)	6	Upper-triangular unipotent matrix group:U(4,2)	5	SmallGroup(32,27)	2	Klein four-group
central product of D8 and Z4	13	48	direct product of S4 and Z2	4	direct product of D8 and Z2	3	elementary abelian group:E8	2	Klein four-group
elementary abelian group:E16	14	20160	alternating group:A8	6	Upper-triangular unipotent matrix group:U(4,2)	0	trivial group	0	trivial group

Subgroup structure

Further information: subgroup structure of groups of order 16