Subnormal-to-normal and normal-to-characteristic: Difference between revisions
No edit summary |
|||
| Line 203: | Line 203: | ||
==Relating subnormal-to-normal and normal-to-characteristic== | ==Relating subnormal-to-normal and normal-to-characteristic== | ||
{ | ===The general form of the relation=== | ||
The properties we discussed in the last two sections: the sort that help us go from subnormal to normal, and the sort that help us go from normal to characteristic, are closely related. They are related by means of the ''left residual'', something we shall try to describe here. | |||
Suppose <math>p, q, r</math> are three [[subgroup property|subgroup properties]]. We say that <math>r</math> is the [[left residual]] of <math>p</math> by <math>q</math> if we have the following: | |||
A subgroup <math>H</math> of a group <math>K</math> has property <math>r</math> in <math>K</math> if and only if for every <math>G</math> containing <math>K</math> such that <math>K</math> has property <math>q</math> in <math>G</math>, <math>H</math> has property <math>p</math> in <math>G</math>. | |||
The left residual of a property by itself is termed its [[left transiter]]. A basic fact is: | |||
[[Left transiter of normal is characteristic]]: A subgroup <math>H</math> of <math>K</math> is characteristic in <math>K</math> if and only if, whenever <math>K</math> is normal in a group <math>G</math>, <math>H</math> is normal in <math>G</math>. | |||
In our case, we observe that the left residual of a subnormal-to-normal property by the property of being a [[normal subgroup]] is a normal-to-characteristic property. If <math>p</math> is the subnormal-to-normal property and <math>r</math> is the normal-to-characteristic property, our general results will be of the form: | |||
* Any subgroup with property <math>r</math> in a normal subgroup has property <math>p</math> in the whole group. | |||
* If <math>H</math> is a subgroup of <math>K</math> such that whenever <math>K</math> is normal in <math>G</math>, <math>H</math> is also normal in <math>G</math>, <math>H</math> has property <math>r</math> in <math>K</math>. | |||
The proofs of all these rely on the fact that [[inner automorphism to automorphism is right tight for normality]]. This states that for any group <math>K</math>, and any automorphism <math>\sigma</math> of <math>K</math>, there exists a group <math>G</math> containing <math>K</math> as a normal subgroup, such that <math>\sigma</math> extends to an [[inner automorphism]] of <math>G</math>. | |||
===Some specific examples of the relation=== | |||
{| class="wikitable" border="1" | |||
!Subnormal-to-normal property !! Left residual, which is a normal-to-characteristic property | |||
|- | |||
| [[Pronormal subgroup]] || [[Procharacteristic subgroup]] | |||
|- | |||
| [[Weakly pronormal subgroup]] | [[Weakly procharacteristic subgroup]] | |||
|- | |||
| [[Paranormal subgroup]] | [[Paracharacteristic subgroup]] | |||
|- | |||
| [[Polynormal subgroup]]| [[Polycharacteristic subgroup]] | |||
|- | |||
| [[Weakly normal subgroup]] | [[Weakly characteristic subgroup]] | |||
|- | |||
|} | |||
In certain situations, we cannot precisely compute the left residual, but can show that a certain property is ''stronger'' than the left residual. For instance: | |||
* [[Intermediately normal-to-characteristic of normal implies intermediately subnormal-to-normal]] | |||
Revision as of 01:12, 16 February 2009
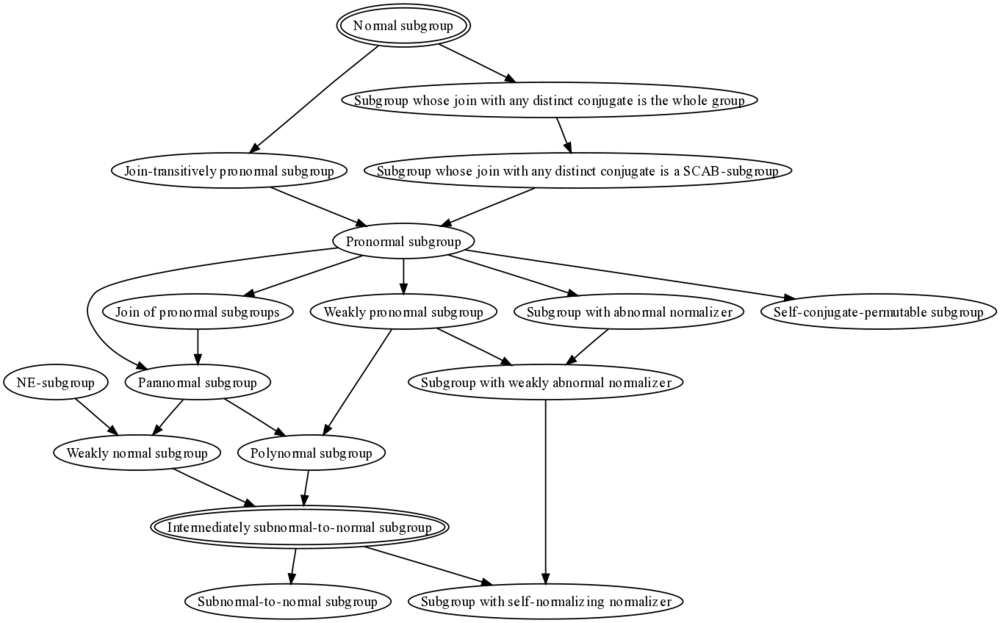
This survey article is about the following three kinds of subgroup properties:
- Subgroup properties that are stronger than the property of being a subnormal-to-normal subgroup. These properties behave as follows: Any subnormal subgroup having the property is a normal subgroup. Most of the properties we discuss here are stronger than the property of being an intermediately subnormal-to-normal subgroup: a subgroup satisfying property has the property that if it is subnormal in any intermediate subgroup, it is also normal in that intermediate subgroup.
- Subgroup properties that are stronger than the property of being a normal-to-characteristic subgroup. These properties behave as follows: any normal subgroup having the property is a characteristic subgroup. Most of the properties we discuss here are stronger than the property of being an intermediately normal-to-characteristic subgroup: a subgroup satisfying property has the property that if it is normal in any intermediate subgroup, it is also characteristic in that intermediate subgroup.
- Subgroup properties such that the only normal subgroup satisfying the property is the whole group (called NCI-subgroup properties on the wiki).
Subnormal-to-normal properties
General remarks
- Most of the properties we discuss here satisfy the intermediate subgroup condition. A subgroup property satisfies the intermediate subgroup condition if whenever are such that satisfies in , also satisfies in .
- Most of the properties here are satisfied by all normal subgroups, and also by all maximal subgroups. None of them is transitive, and in fact, the subordination of any of these properties (i.e., the transitive closed with respect to inclusion) is usually satisfies for all subgroups of finite groups.
- Most of the properties here are not closed under intersections. Some are closed under joins, and many are closed under normalizing joins. A subgroup property is normalizing join-closed if whenever are such that both satisfy and , the join also satisfies .
We will follow a right-action convention to denote conjugation. Thus, , will be termed the conjugate of by . In the left-action convention, is the conjugate of by . To use the left-action convention, replace by and reverse the order of terms in products.
Pronormal subgroup
Further information: Pronormal subgroup
A subgroup of a group is termed pronormal in if, for any , there exists such that .
Any normal subgroup is pronormal, and any maximal subgroup is pronormal. More generally, there are several properties between the property of being normal or maximal and the property of being pronormal. Here are some of them:
- Subgroup whose join with any distinct conjugate is the whole group: Both normal and maximal subgroups satisfy this property, and this property in turn is stronger than pronormality. For full proof, refer: Join with any distinct conjugate is the whole group implies pronormal
- Subgroup whose join with any distinct conjugate is a SCAB-subgroup: This is weaker than the previous property, but still stronger than the property of being pronormal.
Pronormality behaves very differently from normality. Some salient facts about it:
- Pronormality satisfies intermediate subgroup condition: Any pronormal subgroup of the whole group is pronormal in every intermediate subgroup.
- Pronormal implies intermediately subnormal-to-normal: A pronormal subgroup that is subnormal in any intermediate subgroup is also normal in that intermediate subgroup.
- Pronormality is not finite-join-closed (a join of pronormal subgroups need not be pronormal), but pronormality is normalizing join-closed: If are pronormal subgroups of and , then is a pronormal subgroup.
- Pronormality is not transitive. A right-transitively pronormal subgroup is a subgroup such that any pronormal subgroup of is pronormal in . Any direct factor, central factor, or more generally, any SCAB-subgroup is a right-transitively pronormal subgroup. For full proof, refer: SCAB implies right-transitively pronormal
- Pronormal implies WNSCDIN: Pronormal subgroups satisfy a strong condition on conjugacy of normal subsets. Any two normal subsets of a pronormal subgroup that are conjugate in the whole group are conjugate in the normalizer of the pronormal subgroup.
- Pronormal implies self-conjugate-permutable: The only conjugate of a pronormal subgroup that permutes with it is itself.
As we shall see further ahead, Sylow subgroups, and more generally, Sylow subgroups of normal subgroups, are pronormal. In fact, many results proved about Sylow subgroups generalize to results about pronormal subgroups.
Weakly pronormal subgroup
Further information: Weakly pronormal subgroup
The condition of being a weakly pronormal subgroup is a slight weakening of the condition of being a pronormal subgroup. Here, instead of looking at the subgroup generated by and one conjugate , we look at the subgroup generated by and the conjugates of by all powers of . This subgroup is denoted . We require that there exist such that .
Paranormal subgroup
Further information: Paranormal subgroup
Paranormality is a weakening of pronormality, but in a somewhat different direction. For pronormality, we insist that there exist such that . For paranormality, we weaken this from requiring the existence of a single element to simply requiring that be a contranormal subgroup inside : in other words, we require that the normal closure of in be .
Here are some salient facts about paranormality:
- Paranormality satisfies intermediate subgroup condition
- Paranormal implies intermediately subnormal-to-normal
- Paranormality is strongly join-closed: The join of an arbitrary collection of paranormal subgroups is paranormal.
- Pronormal implies paranormal, Paranormal not implies pronormal
Polynormal subgroup
Further information: Polynormal subgroup
Polynormality is a weakening of pronormality that combines the previous two weakenings. is polynormal in if, for any , is a contranormal subgroup of .
Pronormality implies both paranormality and weak pronormality, and both of these imply polynormality. No example of a finite group is known where a polynormal subgroup is not paranormal.
Here are some salient facts about polynormality:
- Polynormality satisfies intermediate subgroup condition
- Polynormal implies intermediately subnormal-to-normal
- Polynormality is strongly join-closed
Weakly normal subgroup
Further information: Weakly normal subgroup
Weak normality is an extremely weak condition; it is weaker than paranormality, though possibly not weaker than polynormality. A subgroup of a group is termed weakly normal in if for any , implies .
Some salient facts about weak normality:
- Weak normality satisfies intermediate subgroup condition
- Weakly normal implies intermediately subnormal-to-normal
- Paranormal implies weakly normal, Weakly normal not implies paranormal
NE-subgroup
Further information: NE-subgroup
The condition of being a NE-subgroup is stronger than weak normality, but is incomparable with paranormality, pronormality, or weak pronormality. Every normal subgroup as well as every self-normalizing subgroup (we'll see more on those later) is a NE-subgroup.
A subgroup of a group is termed a NE-subgroup if equals the intersection of its normalizer and normal closure in .
Some salient facts about NE-subgroups:
- NE satisfies intermediate subgroup condition
- NE implies weakly normal, NE implies intermediately subnormal-to-normal
- NE not implies paranormal, Sylow not implies NE, pronormal not implies NE, paranormal not implies NE
Intermediately subnormal-to-normal subgroup
Further information: intermediately subnormal-to-normal subgroup
A subgroup of a group is termed intermediately subnormal-to-normal in if whenever is a subgroup of containing , and is a subnormal subgroup of , is also a normal subgroup of . This is equivalent to demanding that whenever is a 2-subnormal subgroup of , is normal in .
All the properties mentioned above are stronger than the property of being intermediately subnormal-to-normal.
Subgroup with self-normalizing normalizer, abnormal normalizer, and weakly abnormal normalizer
Further information: subgroup with self-normalizing normalizer, subgroup with abnormal normalizer, subgroup with weakly abnormal normalizer
A subgroup of a group is termed a subgroup with self-normalizing normalizer if . We can have 2-subnormal subgroups, and more generally, subnormal subgroups of arbitrarily large subnormal depth, that have self-normalizing normalizers. Closely related is the property of being a subgroup with abnormal normalizer (the normalizer of the subgroup is an abnormal subgroup), and being a subgroup with weakly abnormal normalizer (the normalizer of the subgroup is a weakly abnormal subgroup). Some important facts:
- Normalizer of pronormal implies abnormal: In particular, a pronormal subgroup is a subgroup with abnormal normalizer.
- Normalizer of weakly pronormal implies weakly abnormal
- Normalizer of intermediately subnormal-to-normal implies self-normalizing
- Abnormal normalizer and 2-subnormal not implies normal: The property of having an abnormal normalizer is insufficient to guarantee that the subgroup is subnormal-to-normal.
Normal-to-characteristic and normal-to-isomorph-free properties
General remarks
For this part, we shall follow the convention of automorphisms acting on the right, by exponentiation. This is to keep consistent with the notation of conjugation on the right. To convert these to analogous statements with automorphisms acting on the left, simply interchange the order of terms in all products.
The properties discussed here are of the kind that, whenever any normal subgroup satisfies the property, it must be a characteristic subgroup. Some of the properties here are even stronger: they are such that whenever any normal subgroup satisfies them, it must be an isomorph-free subgroup.
Some of these properties have this behavior in intermediate subgroups as well: whenever a subgroup with the property is normal in an intermediate subgroup, it is characteristic (or isomorph-free) in that intermediate subgroup.
One of the things that makes the implications messier is that characteristicity does not satisfy intermediate subgroup condition: in other words, a subgroup that is characteristic in the whole group need not be characteristic in every intermediate subgroup. On the other hand, the property of being an isomorph-free subgroup does satisfy the intermediate subgroup condition.
Isomorph-free subgroup, isomorph-containing subgroup
Further information: isomorph-free subgroup, isomorph-containing subgroup
A subgroup of a group is termed an isomorph-free subgroup if any subgroup of isomorphic to is actually equal to . . is termed an isomorph-containing subgroup of if any subgroup of isomorphic to is contained in .
For finite subgroups, and more generally for co-Hopfian subgroups, the two properties are equivalent.
Some salient points about these properties:
- Both these properties satisfy the intermediate subgroup condition. In other words, if and satisfies the property in , also satisfies the property in .
- Both these properties are stronger than the property of being a characteristic subgroup. In particular, they imply the property of being an intermediately characteristic subgroup: being characteristic in every intermediate subgroup.
Isomorph-conjugate and automorph-conjugate subgroups
Further information: isomorph-conjugate subgroup, automorph-conjugate subgroup
We say that is isomorph-conjugate in if any subgroup of isomorphic to is conjugate to . Similarly, we say that is automorph-conjugate in if any subgroup of that is automorphic to (i.e., is the image of under an automorphism of ) is conjugate to .
We have the following:
- Neither the property of being isomorph-conjugate nor the property of being automorph-conjugate satisfy the intermediate subgroup condition. In other words, we can have such that is isomorph-conjugate in but not in .
- Every isomorph-free subgroup is isomorph-conjugate, and any characteristic subgroup is automorph-conjugate.
- For a normal subgroup, being isomorph-conjugate is equivalent to being isomorph-free, and being automorph-conjugate is equivalent to being characteristic.
Intermediately characteristic, intermediately isomorph-conjugate and intermediately automorph-conjugate
Further information: intermediately characteristic subgroup, intermediately isomorph-conjugate subgroup, intermediately automorph-conjugate subgroup
We define the following for a subgroup of a group :
- is intermediately characteristic in if is characteristic in every intermediate subgroup.
- is intermediately isomorph-conjugate in if is isomorph-conjugate in every intermediate subgroup.
- is intermediately automorph-conjugate in if is automorph-conjugate in every intermediate subgroup.
Notice that, since any normal subgroup that is automorph-conjugate (resp., isomorph-conjugate) is in fact characteristic (resp., isomorph-free), each of these properties is stronger than the property of being an intermediately normal-to-characteristic subgroup.
Procharacteristic and weakly procharacteristic
Further information: procharacteristic subgroup, weakly procharacteristic subgroup, intermediately procharacteristic subgroup
Procharacteristicity is something like being automorph-conjugate in every intermediate subgroup, except that it is somewhat different. For the definition of procharacteristicity, we require that the automorphism be only in the ambient group, while conjugacy be checked in intermediate subgroups. Specifically:
A subgroup of a group is termed procharacteristic if, for any automorphism of , there exists such that .
We have a similar definition for a weakly procharacteristic subgroup:
A subgroup of a group is termed procharacteristic if, for any automorphism of , there exists such that .
Some salient points:
- Any intermediately isomorph-conjugate subgroup is procharacteristic. Any characteristic subgroup is also procharacteristic.
- Procharacteristicity does not satisfy the intermediate subgroup condition. A subgroup that is procharacteristic in every intermediate subgroup is termed an intermediately procharacteristic subgroup. Any intermediately characteristic subgroup, and any intermediately isomorph-conjugate subgroup, is intermediately procharacteristic.
- An intermediately automorph-conjugate subgroup need not be procharacteristic. Conversely, a procharacteristic subgroup need not be intermediately automorph-conjugate. Further information: Intermediately automorph-conjugate not implies procharacteristic
- An intermediately automorph-conjugate subgroup must be weakly procharacteristic. In fact, a subgroup is intermediately automorph-conjugate if and only if it is weakly procharacteristic in every intermediate subgroup.
- Any weakly procharacteristic subgroup, and hence any procharacteristic subgroup, is an automorph-conjugate subgroup.
Paracharacteristic, polycharacteristic, intermediately paracharacteristic, and intermediately polycharacteristic
Further information: paracharacteristic subgroup, polycharacteristic subgroup, intermediately paracharacteristic subgroup, ntermediately polycharacteristic subgroup
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]
Weakly characteristic and intermediately weakly characteristic
Further information: weakly characteristic subgroup, intermediately weakly characteristic subgroup
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]
Relating subnormal-to-normal and normal-to-characteristic
The general form of the relation
The properties we discussed in the last two sections: the sort that help us go from subnormal to normal, and the sort that help us go from normal to characteristic, are closely related. They are related by means of the left residual, something we shall try to describe here.
Suppose are three subgroup properties. We say that is the left residual of by if we have the following:
A subgroup of a group has property in if and only if for every containing such that has property in , has property in .
The left residual of a property by itself is termed its left transiter. A basic fact is:
Left transiter of normal is characteristic: A subgroup of is characteristic in if and only if, whenever is normal in a group , is normal in .
In our case, we observe that the left residual of a subnormal-to-normal property by the property of being a normal subgroup is a normal-to-characteristic property. If is the subnormal-to-normal property and is the normal-to-characteristic property, our general results will be of the form:
- Any subgroup with property in a normal subgroup has property in the whole group.
- If is a subgroup of such that whenever is normal in , is also normal in , has property in .
The proofs of all these rely on the fact that inner automorphism to automorphism is right tight for normality. This states that for any group , and any automorphism of , there exists a group containing as a normal subgroup, such that extends to an inner automorphism of .
Some specific examples of the relation
| Subnormal-to-normal property | Left residual, which is a normal-to-characteristic property |
|---|---|
| Pronormal subgroup | Procharacteristic subgroup |
| Weakly pronormal subgroup | Weakly procharacteristic subgroup | |
| Paranormal subgroup | Paracharacteristic subgroup | |
| Polynormal subgroup| Polycharacteristic subgroup | |
| Weakly normal subgroup | Weakly characteristic subgroup |
In certain situations, we cannot precisely compute the left residual, but can show that a certain property is stronger than the left residual. For instance: