Linear representation theory of symmetric group:S4
This article gives specific information, namely, linear representation theory, about a particular group, namely: symmetric group:S4.
View linear representation theory of particular groups | View other specific information about symmetric group:S4
This article discusses the linear representation theory of symmetric group:S4, a group of order 24. In the article we take to be the group of permutations on the set .
Summary
| Item | Value |
|---|---|
| Degrees of irreducible representations over a splitting field | 1,1,2,3,3 maximum: 3, lcm: 6, number: 5, sum of squares: 24, quasirandom degree: 1 |
| Schur index values of irreducible representations | 1,1,1,1,1 maximum: 1, lcm: 1 |
| Smallest ring of realization for all irreducible representations (characteristic zero) | Same as ring generated by character values |
| Smallest field of realization for all irreducible representations, i.e., minimal splitting field (characteristic zero) | (hence it is a rational representation group) Same as field generated by character values |
| Condition for being a splitting field for this group | Any field of characteristic not two or three is a splitting field. |
| minimal splitting field in characteristic | prime field |
| Smallest size splitting field | Field:F5, i.e., the field with five elements. |
Family contexts
| Family name | Parameter values | General discussion of linear representation theory of family |
|---|---|---|
| symmetric group of degree | , i.e., it is the group | linear representation theory of symmetric groups |
| projective general linear group of degree two over a finite field size | , i.e., field:F3, so the group is . | linear representation theory of projective general linear group of degree two |
COMPARE AND CONTRAST: View linear representation theory of groups of order 24 to compare and contrast the linear representation theory with other groups of order 24.
Back story
This page gives information about the degrees of irreducible representations, character table, and irreducible linear representations of symmetric group:S4. It does not, however, provide an adequate explanation of how one might arrive at (i.e., deduce) the information. For more on the back story, see determination of character table of symmetric group:S4.
Irreducible representations
Summary information
Below is summary information on irreducible representations that are absolutely irreducible, i.e., they remain irreducible in any bigger field, and in particular are irreducible in a splitting field. We assume that the characteristic of the field is not 2 or 3, except in the last two columns, where we consider what happens in characteristic 2 and characteristic 3.
| Name of representation type | Number of representations of this type | Degree | Schur index | Criterion for field | Kernel | Quotient by kernel (on which it descends to a faithful representation) | Characteristic 2 | Characteristic 3 |
|---|---|---|---|---|---|---|---|---|
| trivial | 1 | 1 | 1 | any | whole group | trivial group | works | works |
| sign | 1 | 1 | 1 | any | A4 in S4 (unless the characteristic is two, in which case it is the whole group) | cyclic group:Z2 (unless the characteristic is two, in which case we get trivial group) | works, same as trivial | works |
| two-dimensional irreducible | 1 | 2 | 1 | any | normal V4 in S4 | symmetric group:S3 | works | indecomposable but not irreducible |
| standard representation of symmetric group:S4 | 1 | 3 | 1 | any | trivial subgroup, i.e., it is faithful | symmetric group:S4 | indecomposable but not irreducible | works |
| product of standard and sign | 1 | 3 | 1 | any | trivial subgroup, i.e., it is faithful | symmetric group:S4 | indecomposable but not irreducible | works |
Trivial representation
This is a one-dimensional representation sending every element of the symmetric group of degree four to the matrix .
Sign representation
This is a one-dimensional representation that sends all even permutations to and all odd permutations to .
Degree two irreducible representation
The symmetric group of degree four has a normal subgroup of order four, namely: (for more, see normal V4 in S4). The quotient by this subgroup is isomorphic to the symmetric group of degree three. The symmetric group of degree three has an irreducible representation of degree two that can be realized over the rationals (namely, its standard representation). Composing the quotient map with this representation of the quotient group gives an irreducible representation of degree two of the symmetric group of degree four.
Standard representation
Further information: standard representation of symmetric group:S4
The two irreducible representations of degree three are: the standard representation (which is the nontrivial irreducible constituent in the natural representation on a -dimensional vector space via permutation of the basis elements) and the tensor product of the standard representation and the sign representation.
The natural representation given by the action on a -dimensional vector space by basis permutation (here ) has character as follows: the character of a permutation is its number of fixed points. We are decomposing this natural representation as a direct sum of the trivial representation and the standard representation. Thus, the character of the standard representation is defined as follows: the character value at a permutation is (number of fixed points) - 1.
Product of standard representation and sign representation
This is the other three-dimensional irreducible representation, and it is the tensor product of the standard representation and the sign representation. The matrix corresponding to a permutation for this representation is the sign of the permutation times the matrix corresponding to the standard representation.
Character table
FACTS TO CHECK AGAINST (for characters of irreducible linear representations over a splitting field):
Orthogonality relations: Character orthogonality theorem | Column orthogonality theorem
Separation results (basically says rows independent, columns independent): Splitting implies characters form a basis for space of class functions|Character determines representation in characteristic zero
Numerical facts: Characters are cyclotomic integers | Size-degree-weighted characters are algebraic integers
Character value facts: Irreducible character of degree greater than one takes value zero on some conjugacy class| Conjugacy class of more than average size has character value zero for some irreducible character | Zero-or-scalar lemma
This is the character table over characteristic zero.
| Representation/Conjugacy class representative and size | (identity element) (size 1) | (size 3) | (size 6) | (size 6) | (size 8) |
|---|---|---|---|---|---|
| Trivial representation | 1 | 1 | 1 | 1 | 1 |
| Sign representation | 1 | 1 | -1 | -1 | 1 |
| Irreducible representation of degree two with kernel of order four | 2 | 2 | 0 | 0 | -1 |
| Standard representation | 3 | -1 | 1 | -1 | 0 |
| Product of standard and sign representations | 3 | -1 | -1 | 1 | 0 |
Note that since all representations are realized over the rational numbers, all characters are integer-valued.
The same character table applies in any characteristic not equal to 2 or 3, where 0,-1,1,2 are interpreted, not as integers, but as elements of that field.
Here are the size-degree weighted characters (i.e., the product of the character value by the size of the conjugacy class divided by the degree of the representation).
| Representation/Conjugacy class representative and size | (identity element) (size 1) | (size 3) | (size 6) | (size 6) | (size 8) |
|---|---|---|---|---|---|
| Trivial representation | 1 | 3 | 6 | 6 | 8 |
| Sign representation | 1 | 3 | -6 | -6 | 8 |
| Irreducible representation of degree two with kernel of order four | 1 | 3 | 0 | 0 | -4 |
| Standard representation | 1 | -1 | 2 | -2 | 0 |
| Product of standard and sign representations | 1 | -1 | -2 | 2 | 0 |
Degrees of irreducible representations
FACTS TO CHECK AGAINST FOR DEGREES OF IRREDUCIBLE REPRESENTATIONS OVER SPLITTING FIELD:
Divisibility facts: degree of irreducible representation divides group order | degree of irreducible representation divides index of abelian normal subgroup
Size bounds: order of inner automorphism group bounds square of degree of irreducible representation| degree of irreducible representation is bounded by index of abelian subgroup| maximum degree of irreducible representation of group is less than or equal to product of maximum degree of irreducible representation of subgroup and index of subgroup
Cumulative facts: sum of squares of degrees of irreducible representations equals order of group | number of irreducible representations equals number of conjugacy classes | number of one-dimensional representations equals order of abelianization
Note that the linear representation theory of the symmetric group of degree four works over any field of characteristic not equal to two or three, and the list of degrees is .
Interpretation as symmetric group
| Common name of representation | Degree | Corresponding partition | Young diagram | Hook-length formula for degree | Quick rule for character computation | Conjugate partition | Representation for conjugate partition |
|---|---|---|---|---|---|---|---|
| trivial representation | 1 | 4 | 1 everywhere | 1 + 1 + 1 + 1 | sign representation | ||
| sign representation | 1 | 1 + 1 + 1 + 1 | 1 on even, -1 on odd permutations | 4 | trivial representation | ||
| degree two irreducible representation | 2 | 2 + 2 |  |
(complicated) | 2 + 2 | same representation because the partition is self-conjugate | |
| standard representation | 3 | 3 + 1 | 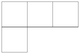 |
(number of fixed points) - 1 | 2 + 1 + 1 | product of standard representation and sign representation | |
| product of standard representation and sign representation | 3 | 2 + 1 + 1 | 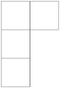 |
(sign) times (number of fixed points - 1) | 3 + 1 | standard representation |
Interpretation as projective general linear group of degree two
Compare and contrast with linear representation theory of projective general linear group of degree two over a finite field
Below is an interpretation of the group as the projective general linear group of degree two over field:F3, the field of three elements.
| Description of collection of representations | Parameter for describing each representation | How the representation is described | Degree of each representation (general | Degree of each representation () | Number of representations (general ) | Number of representations () | Sum of squares of degrees (general ) | Sum of squares of degrees () | Symmetric group name |
|---|---|---|---|---|---|---|---|---|---|
| Trivial | -- | 1 | 1 | 1 | 1 | 1 | 1 | trivial | |
| Sign representation | -- | Kernel is projective special linear group of degree two (in this case, alternating group:A4), image is | 1 | 1 | 1 | 1 | 1 | 1 | sign |
| Unclear | a nontrivial homomorphism (or more generally, to the multiplicative group of the field where we're taking representations), with the property that for all , and takes values other than . Identify and . | unclear | 2 | 1 | 4 | degree two irreducible | |||
| Nontrivial component of permutation representation of on the projective line over | -- | -- | 3 | 1 | 1 | 9 | standard | ||
| Tensor product of sign representation and nontrivial component of permutation representation on projective line | -- | -- | 3 | 1 | 1 | 9 | product of sign and standard | ||
| Induced from one-dimensional representation of Borel subgroup | -- | -- | 4 | 0 | 0 | -- | |||
| Total | NA | NA | NA | NA | 5 | 24 | NA |
Realizability information
Smallest ring of realization
| Representation | Smallest ring of realization | Smallest set of elements occurring as matrix entries in the ring |
|---|---|---|
| trivial representation | -- ring of integers | |
| sign representation | -- ring of integers | |
| representation with kernel of order four | -- ring of integers | |
| standard representation | -- ring of integers | |
| product of standard and alternating representations | -- ring of integers |
Smallest ring of realization as orthogonal matrices
| Representation | Smallest ring of realization |
|---|---|
| trivial representation | -- ring of integers |
| sign representation | -- ring of integers |
| representation with kernel of order four |
Schur functors corresponding to irreducible representations
Note that the discussion in this section relies specifically on the group being a symmetric group, and does not make sense for arbitrary finite groups.
| Common name of representation | Degree | Square of degree | Corresponding partition | Young diagram | Common name of corresponding Schur functor | Formula for dimension of corresponding Schur functor applied to a vector space of dimension | Degree of representation times this dimension | Formula for calculating effect of Schur functor on character if this Schur functor is applied to any (possibly unrelated) representation whose character is |
|---|---|---|---|---|---|---|---|---|
| trivial representation | 1 | 1 | 4 | PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE] | ||||
| sign representation | 1 | 1 | 1 + 1 + 1 + 1 | PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE] | ||||
| degree two irreducible representation | 2 | 4 | 2 + 2 |  |
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE] | |||
| standard representation | 3 | 9 | 3 + 1 |  |
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE] | |||
| product of standard representation and sign representation | 3 | 9 | 2 + 1 + 1 |  |
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE] | |||
| Total | 24 (equals 4!, order of group) | -- | -- | -- | -- | (equals dimension of ) | -- |
Character ring structure
FACTS TO CHECK AGAINST (character ring):
Sums and products: character of direct sum of linear representations is sum of characters|character of tensor product of linear representations is product of characters
Tensor products and irreducibility: tensor product of irreducible representation and one-dimensional representation is irreducible| tensor product of irreducible representations need not be irreducible
This describes the decomposition of products of characters as sums of characters. This is:
| Representation/representation | trivial | sign | irreducible of degree two | standard | product of standard and sign |
|---|---|---|---|---|---|
| trivial | trivial | sign | irreducible of degree two | standard | product of standard and sign |
| sign | sign | trivial | irreducible of degree two | product of standard and sign | standard |
| irreducible of degree two | irreducible of degree two | irreducible of degree two | irreducible of degree two + trivial + sign | standard + product of standard and sign | standard + product of standard and sign |
| standard | standard | product of standard and sign | standard + product of standard and sign | trivial + irreducible of degree two + standard + product of standard and sign | sign + irreducible of degree two + standard + product of standard and sign |
| product of standard and sign | product of standard and sign | standard | standard + product of standard and sign | sign + irreducible of degree two + standard + product of standard and sign | trivial + irreducible of degree two + standard + product of standard and sign |
Orthogonality relations and numerical checks
| General statement | Verification in this case |
|---|---|
| number of irreducible representations equals number of conjugacy classes | Both numbers in this case are equal to 5. As symmetric group: Both numbers are equal to the number of unordered integer partitions of 4. As projective general linear group : Both numbers are equal to . |
| sufficiently large implies splitting: if the field has characteristic not dividing the order of the group and has primitive roots of unity for the exponent of the group, it is a splitting field. | In fact, for this group, any field of characteristic not 2 or 3 is a splitting field. |
| number of one-dimensional representations equals order of abelianization | Both numbers are equal to 2: the representations are the trivial and sign representation. The derived subgroup is A4 in S4, which has index two. |
| sum of squares of degrees of irreducible representations equals group order | As symmetric group: follows from the Robinson-Schensted correspondence As projective general linear group: See linear representation theory of projective general linear group of degree two over a finite field |
| degree of irreducible representation divides order of group | All the degrees divide the group order which is |
| degree of irreducible representation divides index of abelian normal subgroup | All the degrees divide 6, the index of normal V4 in S4, the only nontrivial abelian normal subgroup |
| row orthogonality theorem and column orthogonality theorem | can be verified from the character table |
Relation with quotients
Symmetric group:S4 has four normal subgroups: the whole group, the trivial subgroup, and two others. The irreducible representations with kernel a particular normal subgroup correspond precisely to the faithful irreducible representations of the quotient group; the irreducible representations with kernel containing a particular normal subgroup correspond precisely to the irreducible representations of the quotient group. Information in this regard is presented below:
| Normal subgroup in whole group | Normal subgroup isomorphism type | Quotient group | Linear representation theory of quotient group | Degrees of irreducible representations of quotient group | List of irreducible representations of quotient group (corresponding representation of whole group) | Degrees of faithful irreducible representations of quotient group | List of faithful irreducible representations of quotient group (corresponding representation of whole group) |
|---|---|---|---|---|---|---|---|
| whole group | symmetric group:S4 | trivial group | 1 | trivial (trivial) | 1 | trivial (trivial) | |
| A4 in S4 | alternating group:A4 | cyclic group:Z2 | link | 1,1 | trivial (trivial), sign (sign) | 1 | sign (sign) |
| normal V4 in S4 | Klein four-group | symmetric group:S3 | link | 1,1,2 | trivial (trivial), sign (sign), standard (becomes two-dimensional irreducible for , not standard for ) | 2 | standard (becomes two-dimensional irreducible for , not standard for ) |
| trivial subgroup | trivial group | symmetric group:S4 | link | 1,1,2,3,3 | trivial (trivial), sign (sign), two-dimensional irreducible (two-dimensional irreducible), standard (standard), product of standard and sign (product of standard and sign) | 3,3 | standard (standard), product of standard and sign (product of standard and sign) |
Relation with subgroups
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]
GAP implementation
Degrees of irreducible representations
The degrees of irreducible representations can be computed using GAP's CharacterDegrees function, as follows:
gap> CharacterDegrees(SymmetricGroup(4)); [ [ 1, 2 ], [ 2, 1 ], [ 3, 2 ] ]
This means that there are two irreducible representations of degree 1, 1 of degree 2, and 2 of degree 3.
Character table
The character table of this group can be computed using GAP's CharacterTable function, as follows:
gap> Irr(CharacterTable("Symmetric",4));
[ Character( CharacterTable( "Sym(4)" ), [ 1, -1, 1, 1, -1 ] ), Character( CharacterTable( "Sym(4)" ), [ 3, -1, -1, 0, 1 ] ),
Character( CharacterTable( "Sym(4)" ), [ 2, 0, 2, -1, 0 ] ), Character( CharacterTable( "Sym(4)" ), [ 3, 1, -1, 0, -1 ] ),
Character( CharacterTable( "Sym(4)" ), [ 1, 1, 1, 1, 1 ] ) ]
A visual display of the character table can be achieved as follows:
gap> Display(CharacterTable(SymmetricGroup(4)));
CT1
2 3 2 3 . 2
3 1 . . 1 .
1a 2a 2b 3a 4a
2P 1a 1a 1a 3a 2b
3P 1a 2a 2b 1a 4a
X.1 1 -1 1 1 -1
X.2 3 -1 -1 . 1
X.3 2 . 2 -1 .
X.4 3 1 -1 . -1
X.5 1 1 1 1 1
Irreducible representations
The matrices of irreducible representations can be computed using GAP's IrreducibleRepresentations function, as follows:
gap> IrreducibleRepresentations(SymmetricGroup(4));
[ Pcgs([ (3,4), (2,4,3), (1,4)(2,3), (1,3)(2,4) ]) -> [ [ [ 1 ] ], [ [ 1 ] ], [ [ 1 ] ], [ [ 1 ] ] ], Pcgs([ (3,4), (2,4,3), (1,4)(2,3), (1,3)(2,4) ]) ->
[ [ [ -1 ] ], [ [ 1 ] ], [ [ 1 ] ], [ [ 1 ] ] ], Pcgs([ (3,4), (2,4,3), (1,4)(2,3), (1,3)(2,4) ]) ->
[ [ [ 0, 1 ], [ 1, 0 ] ], [ [ E(3), 0 ], [ 0, E(3)^2 ] ], [ [ 1, 0 ], [ 0, 1 ] ], [ [ 1, 0 ], [ 0, 1 ] ] ],
Pcgs([ (3,4), (2,4,3), (1,4)(2,3), (1,3)(2,4) ]) -> [ [ [ 0, 1, 0 ], [ 1, 0, 0 ], [ 0, 0, 1 ] ], [ [ 0, 0, 1 ], [ 1, 0, 0 ], [ 0, 1, 0 ] ],
[ [ -1, 0, 0 ], [ 0, 1, 0 ], [ 0, 0, -1 ] ], [ [ 1, 0, 0 ], [ 0, -1, 0 ], [ 0, 0, -1 ] ] ], Pcgs([ (3,4), (2,4,3), (1,4)(2,3), (1,3)(2,4) ]) ->
[ [ [ 0, -1, 0 ], [ -1, 0, 0 ], [ 0, 0, -1 ] ], [ [ 0, 0, 1 ], [ 1, 0, 0 ], [ 0, 1, 0 ] ], [ [ -1, 0, 0 ], [ 0, 1, 0 ], [ 0, 0, -1 ] ],
[ [ 1, 0, 0 ], [ 0, -1, 0 ], [ 0, 0, -1 ] ] ] ]
Note that this only gives the matrices of images of a generating set.














































![{\displaystyle \mathbb {Z} [{\sqrt {3}}/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e84b55db819bd29b04ae6814b028ac142aed27fa)




















