Classification of groups of prime-cube order

Statement

Let be a prime number. Then there are, up to isomorphism, five groups of order . These include three abelian groups and two non-abelian groups. The nature of the two non-abelian groups is somewhat different for the case .

For more information on side-by-side comparison of the groups for odd primes, see groups of prime-cube order. For information for the prime 2, see groups of order 8

The three abelian groups

The three abelian groups correspond to the three partitions of 3:

Partition of 3	Corresponding abelian group	GAP ID among groups of order
3	cyclic group of prime-cube order, denoted or , or	1
2 + 1	direct product of cyclic group of prime-square order and cyclic group of prime order, denoted or	2
1 + 1 + 1	elementary abelian group of prime-cube order, denoted , or , or	5

The two non-abelian groups

For the case , these are dihedral group:D8 (GAP ID: (8,3)) and quaternion group (GAP ID: (8,4)).

For the case of odd , these are unitriangular matrix group:UT(3,p) (GAP ID: (,3)) and semidirect product of cyclic group of prime-square order and cyclic group of prime order (GAP ID: (,4)).

Related facts

• Classification of nilpotent Lie rings of prime-cube order
• Classification of groups of prime-square order
• Classification of Lie rings of prime-square order

Facts used

The table below lists key facts used directly and explicitly in the proof. Fact numbers as used in the table may be referenced in the proof. This table need not list facts used indirectly, i.e., facts that are used to prove these facts, and it need not list facts used implicitly through assumptions embedded in the choice of terminology and language.

Fact no.	Statement	Steps in the proof where it is used	Qualitative description of how it is used	What does it rely on?	Difficulty level	Other applications
1	Prime power order implies not centerless	Step (CD1)	Eliminates the case of trivial center	class equation of a group	3	click here
2	Center is normal	Steps (CD2), (CD4)	Used to note that the quotient by the center exists as a group		0	click here
3	Cyclic over central implies abelian	Steps (CD2) (CD4)	Rules out the possibility of center of order , helps determine nature of quotient group if center has order			click here
4	Lagrange's theorem	Step (CD2)	Narrows down possibilities for order of center, and allows for computation of order of quotient group		2	click here
5	Equivalence of definitions of group of prime order: This basically states that any group of prime order must be cyclic.	Steps (CD2), (CD4)	Helps rule out center of order , helps determine isomorphism class of center of order			click here
6	Classification of groups of prime-square order	Step (CD4)	Narrows down possibilities for quotient by the center once we have determined that the center has order		3	click here
7	Structure theorem for finitely generated abelian groups	Classification of abelian groups case				click here
8	Class two implies commutator map is endomorphism	Case B analysis	Helps reduce general case to a specific presentation by a change of variable		|| click here
9	Formula for powers of product in group of class two	Case C analysis	Helps reduce Case C to Case B by a change of variable		|| click here

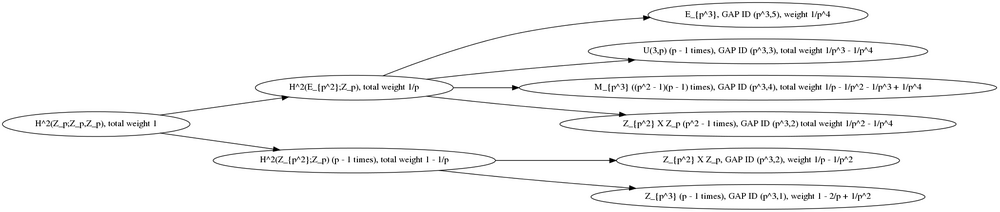
Cohomology tree

This can be formulated as an alternative proof if we prove assertions for each of the cohomology groups.

For odd primes

The cohomology groups governing the branchings are as follows:

• Second cohomology group for trivial group action of group of prime order on group of prime order controls the initial branching from the root.
• Second cohomology group for trivial group action of elementary abelian group of prime-square order on group of prime order controls the upper second level branching.
• Second cohomology group for trivial group action of cyclic group of prime-square order on group of prime order controls the lower second level branching.

For the prime 2

This is for groups of order 8:

The cohomology groups governing the branchings are as follows:

• Second cohomology group for trivial group action of Z2 on Z2 controls the initial branching from the root.
• Second cohomology group for trivial group action of V4 on Z2 controls the upper second level branching.
• Second cohomology group for trivial group action of Z4 on Z2 controls the lower second level branching.

Proof

This proof uses a tabular format for presentation. Provide feedback on tabular proof formats in a survey (opens in new window/tab) | Learn more about tabular proof formats|View all pages on facts with proofs in tabular format

First part of proof: crude descriptions of center and quotient by center

Given: A prime number , a group of order .

To prove: Either is abelian, or we have: is a cyclic group of order and is an elementary abelian group of order

Proof: Let be the center of .

Step no.	Assertion/construction	Facts used	Given data used	Previous steps used	Explanation
CD1	is nontrivial	Fact (1)	has order , specifically, a power of a prime		Fact+Given direct
CD2	The order of cannot be	Facts (2), (3), (4), (5)	has order		[SHOW MORE] exists by fact (2) and has order by fact (4). If has order , the order of is . By fact (5), must be cyclic. Then, by fact (3), would be abelian, but this would imply that , in which case the order of would have been .
CD3	The order of is either or	Fact (4)	has order	Steps (CD1), (CD2)	[SHOW MORE] By fact (4), the order of must divide the order of . The only possibilities are . Step (CD1) eliminates the possibility of , and step (CD2) eliminates the possibility of . This leaves only or .
CD4	If has order , then is cyclic of order and the quotient is elementary abelian of order	Facts (2), (3), (4), (5), (6)	has order .		[SHOW MORE] If has order , then by fact (5), must be cyclic. exists by Fact (2) and its order is by Fact (4). By fact (3), cannot be cyclic, because if it were cyclic, then would be abelian, which would mean that has order . Thus, is a non-cyclic group of order . By fact (6), the only non-cyclic group of order is the elementary abelian group, so must be the elementary abelian group of order .
CD5	If has order , is abelian.		has order .		[SHOW MORE] We get , so is abelian.
CD6	We get the desired result.			Steps (CD3), (CD4), (CD5)	Step-combination.

Second part of proof: classifying the abelian groups

This classification follows from fact (7): the abelian groups of order correspond to partitions of 3, as indicated in the original statement of the classification.

Third part of proof: classifying the non-abelian groups

Given: A non-abelian group of order . Let be the center of .

Previous steps: is cyclic of order , and is elementary abelian of order .

We first make some additional observations.

Step no.	Assertion/construction	Facts used	Given data used	Previous steps used	Explanation
CN1	The derived subgroup (commutator subgroup) equals , so has class two.		is non-abelian of order .	is abelian, has order .	[SHOW MORE] Since is abelian, is contained in . Since has prime order, the only possible subgroups are the trivial subgroup and itself. The derived subgroup cannot be trivial since is non-abelian, hence the derived subgroup must be . Note that this forces to have class two.
CN2	We can find elements such that the images of in are non-identity elements of that generate it.			is elementary abelian of order	[SHOW MORE] is elementary abelian of order , hence is generated by a set of size two comprising non-identity elements. Choose to be arbitrary inverse images of these elements.
CN3	together generate .			Step (CN2)
CN4	and do not commute.			Steps (CN2), (CN3)	[SHOW MORE] If and commute, then contains , hence equals all of . Thus, , so its image in is the identity element, a contradiction to what we assumed.
CN5	Let . Then, is a non-identity element of and .			Steps (CN1), (CN4)	[SHOW MORE] We must have , which equals by Step (1). By Step (4), is not the identity element. So is a non-identity element of . Further, since has order , it has no proper nontrivial subgroups, so must equal all of .
CN6	The elements both have order either or . Also, the elements and are both in .				[SHOW MORE] The order of must divide the order of the group, which is . It cannot equal , because that would make the group cyclic and hence abelian. It cannot equal , because is a non-identity element. The only possibilities are and . Also, the image of in has order because is elementary abelian, so . The same goes for .

We now make cases based on the orders of and . Note that these cases may turn out to yield isomorphic groups, because the cases are made based on and , and there is some freedom in selecting these.

Case A: and both have order .

In this case, the relations so far give the presentation:

These relations already restrict us to order at most , because we can use the commutation relations to express every element in the form , where are integers mod . To show that there is no further reduction, we note that there is a group of order satisfying all these relations, namely unitriangular matrix group:UT(3,p). This is the multiplicative group of unipotent upper-triangular matrices with entries from the field of elements.

Thus, Case A gives a unique isomorphism class of groups. Note that the analysis so far works both for and for odd primes. The nature of the group obtained, though, is different for , where we get dihedral group:D8 which has exponent . For odd primes, we get a group of prime exponent.

Case B: has order , has order

In this case, we first note that . Since is a non-identity element, there exists nonzero (taken mod ) such that . Consider the element Then, by Fact (8), and the observation that has class two (Step (1) in the above table), we obtain:

Consider the presentation:

We see that all these relations are forced by the above, and further, that this presentation defines a group of order , namely semidirect product of cyclic group of prime-square order and cyclic group of prime order.

Thus, there is a unique isomorphism class in Case B. Note that the analysis so far works both for and for odd primes. The nature of the group, though, is different for , we get dihedral group:D8, which is the same isomorphism class as Case A.

Case B2: has order , has order .

Interchange the roles of and replace by and we are back in Case B.

Case C: and both have order .

By Fact (9), we can show that for odd prime, it is possible to make a substitution and get into Case B. PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]

One of the people editing this page intended to fill in this information at a later stage, but hasn't gotten around to doing it yet. If you see this placeholder for a long time, file an error report at the error reporting page.

For , working out the presentation yields quaternion group.

Here is a summary of the cases:

Case letter	What it means	Isomorphism class of group for	Isomorphism class of group for odd prime
A	Both have order	dihedral group:D8	unitriangular matrix group:UT(3,p)
B, B2	One of the elements has order , the other has order	dihedral group:D8	semidirect product of cyclic group of prime-square order and cyclic group of prime order
C	Both elements have order	quaternion group	semidirect product of cyclic group of prime-square order and cyclic group of prime order

Finally, we note that:

• Dihedral group:D8 and quaternion group are non-isomorphic: The latter has no non-central element of order two, for instance.
• Unitriangular matrix group:UT(3,p) and semidirect product of cyclic group of prime-square order and cyclic group of prime order are non-isomorphic: The former has exponent , the latter has exponent .