Subgroup structure of groups of order 16

This article gives specific information, namely, subgroup structure, about a family of groups, namely: groups of order 16.
View subgroup structure of group families | View subgroup structure of groups of a particular order |View other specific information about groups of order 16

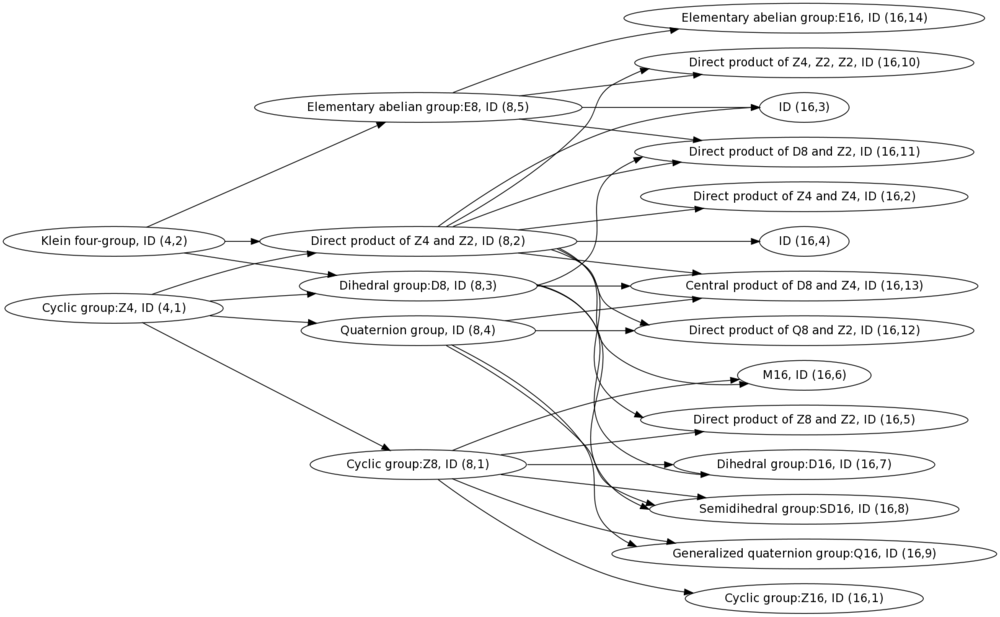
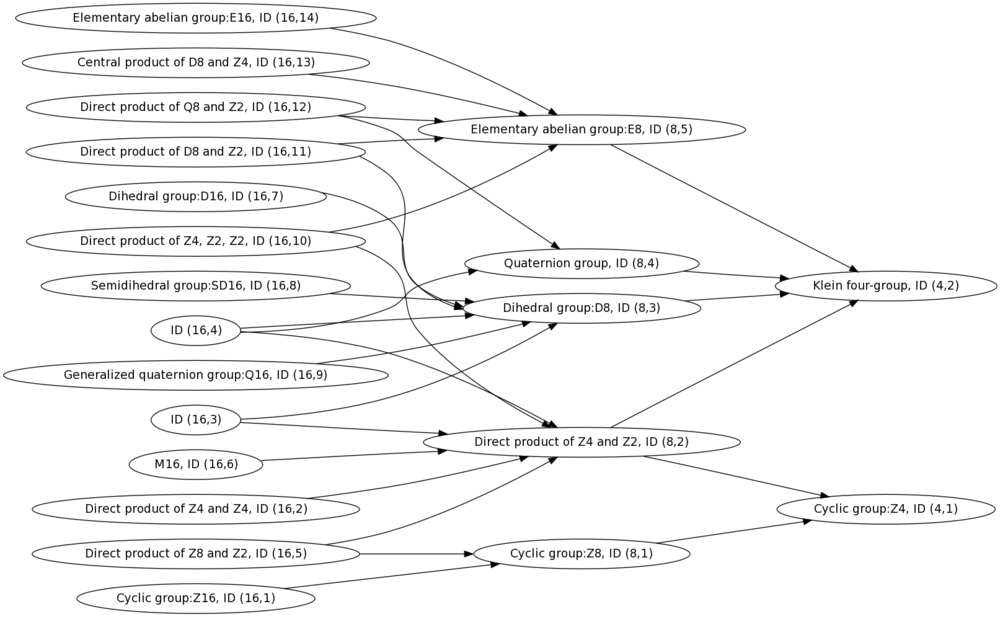
Subgroup/quotient relationships

Subgroup relationships

Quotient relationships

Possibilities for maximal subgroups

Collection of isomorphism classes of maximal subgroups	Groups
cyclic group:Z8	cyclic group:Z16
direct product of Z4 and Z2	direct product of Z4 and Z4, SmallGroup(16,4)
elementary abelian group:E8	elementary abelian group:E16
cyclic group:Z8, direct product of Z4 and Z2	direct product of Z8 and Z2, M16
cyclic group:Z8, dihedral group:D8	dihedral group:D16
cyclic group:Z8, dihedral group:D8, quaternion group	semidihedral group:SD16
cyclic group:Z8, quaternion group	generalized quaternion group:Q16
direct product of Z4 and Z2, elementary abelian group:E8	direct product of Z4 and V4, SmallGroup(16,3)
direct product of Z4 and Z2, elementary abelian group:E8, dihedral group:D8	direct product of D8 and Z2
direct product of Z4 and Z2, quaternion group	direct product of Q8 and Z2
dihedral group:D8, quaternion group, direct product of Z4 and Z2	central product of D8 and Z4

Numerical information on counts of subgroups by isomorphism type

FACTS TO CHECK AGAINST FOR SUBGROUP STRUCTURE: (group of prime power order)
Lagrange's theorem (order of subgroup times index of subgroup equals order of whole group, so all subgroups have prime power orders)|order of quotient group divides order of group (and equals index of corresponding normal subgroup, so all quotients have prime power orders)
prime power order implies not centerless | prime power order implies nilpotent | prime power order implies center is normality-large
size of conjugacy class of subgroups divides index of center
congruence condition on number of subgroups of given prime power order: The total number of subgroups of any fixed prime power order is congruent to 1 mod the prime.

Number of subgroups per isomorphism type

The number in each column is the number of subgroups in the given group of that isomorphism type:

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	Nilpotency class	cyclic group:Z2	cyclic group:Z4	Klein four-group	cyclic group:Z8	direct product of Z4 and Z2	dihedral group:D8	quaternion group	elementary abelian group:E8	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z16	1	5	$(4)$	1	1	1	0	1	0	0	0	0	5
direct product of Z4 and Z4	2	3	$(2^{2})$	1	3	6	1	0	3	0	0	0	15
SmallGroup(16,3)	3	9	$16\Gamma _{2}c_{1}$	2	7	4	7	0	2	0	0	1	23
nontrivial semidirect product of Z4 and Z4	4	10	$16\Gamma _{2}c_{2}$	2	3	6	1	0	3	0	0	0	15
direct product of Z8 and Z2	5	4	$(31)$	1	3	2	1	2	1	0	0	0	11
M16	6	11	$16\Gamma _{2}d$	2	3	2	1	2	1	0	0	0	11
dihedral group:D16	7	12	$16\Gamma _{3}a_{1}$	3	9	1	4	1	0	2	0	0	19
semidihedral group:SD16	8	13	$16\Gamma _{3}a_{2}$	3	5	3	2	1	0	1	1	0	15
generalized quaternion group:Q16	9	14	$16\Gamma _{3}a_{3}$	3	1	5	0	1	0	0	2	0	11
direct product of Z4 and V4	10	2	$(21^{2})$	1	7	4	7	0	6	0	0	1	27
direct product of D8 and Z2	11	6	$16\Gamma _{2}a_{1}$	2	11	2	13	0	1	4	0	2	35
direct product of Q8 and Z2	12	7	$16\Gamma _{2}a_{2}$	2	3	6	1	0	3	0	4	0	19
central product of D8 and Z4	13	8	$16\Gamma _{2}b$	2	7	4	3	0	3	3	1	0	23
elementary abelian group:E16	14	1	$(1^{5})$	1	15	0	35	0	0	0	0	15	67
Total	--	--	--	--	78	46	76	8	23	10	8	19	296
Average	--	--	--	--	5.5714	3.2857	5.4286	0.5714	1.6429	0.7143	0.5714	1.3571	21.1429