Thompson's replacement theorem for abelian subgroups

This article defines a replacement theorem
View a complete list of replacement theorems| View a complete list of failures of replacement

Statement

Suppose $P$ is a group of prime power order (we'll call the prime $p$ ).

Let ${\mathcal {A}}(P)$ denote the set of all abelian subgroups of maximum order in $P$ (i.e., $|A|\geq |B|$ for all abelian subgroups $B$ of $P$ ).

Suppose $A\in {\mathcal {A}}(P)$ and $B$ is an abelian subgroup such that $A$ normalizes $B$ but $B$ does not normalize $A$ . Then, there exists an abelian subgroup $A^{*}$ of $AB$ such that:

$A^{*}\in {\mathcal {A}}(P)$ .
$A\cap B$ is a proper subgroup of $A^{*}\cap B$ .
$A^{*}$ is contained in $\langle A^{B}\rangle =\langle A^{AB}\rangle$ , i.e., it is contained in the normal closure of $A$ in $AB$ . In particular, it is contained in the normal closure $\langle A^{P}\rangle$ of $A$ in $P$ .
$A^{*}$ normalizes $A$ .

We have the following additional conclusions:

$A^{*}$ normalizes $B$ : Note that since $A^{*}$ is contained in $AB$ , and $AB\leq N_{P}(B)$ by assumption, we see that $A^{*}$ normalizes $B$ as well.
$A^{*}\cap B$ is a proper subgroup of $B$ : This is because $A^{*}$ cannot contain $B$ , since $A^{*}$ normalizes $A$ but $B$ does not normalize $A$ .

Thus, all the conditions assumed for $A$ also hold for $A^{*}$ , except possibly the fact that $B$ does not normalize $A$ . Hence, the term replacement.

Related facts

Similar replacement theorems

For a complete list of replacement theorems, refer:

Category:Replacement theorems

Applications

Stable version of Thompson's replacement theorem for abelian subgroups: This is a result obtained via repeated application of Thompson's replacement theorem as long as $B$ does not normalize the (replaced) $A$ .
Any abelian normal subgroup normalizes an abelian subgroup of maximum order
There exists an abelian subgroup of maximum order whose normalizer contains every abelian subgroup it normalizes

Facts used

Proof

This proof uses a tabular format for presentation. Provide feedback on tabular proof formats in a survey (opens in new window/tab) | Learn more about tabular proof formats|View all pages on facts with proofs in tabular format

Given: A finite $p$ -group $P$ . ${\mathcal {A}}(P)$ is the set of abelian subgroups of $P$ of maximum order. $A\in {\mathcal {A}}(P)$ , and $B$ is a subgroup of $A$ such that $A$ normalizes $B$ but $B$ does not normalize $A$ .

To prove: There exists $A^{*}\in {\mathcal {A}}(P)$ such that $A\cap B$ is a proper subgroup of $A^{*}\cap B$ , $A^{*}$ normalizes $A$ and $B$ , and $A^{*}$ is contained in $AB$ .

Proof: We let $C=AB$ and $N=N_{B}(A)$ .

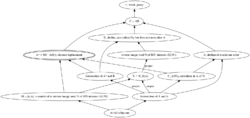
basic diagram of key initial constructions (steps 1-6)

Step no.	Assertion	Facts used	Given data used	Proof steps used	Explanation
1	$C=AB$ is a subgroup of $P$ , and $B$ is normal in $C$	--	$A$ normalizes $B$	--	[SHOW MORE] $C=AB$ is a subgroup since $A$ normalizes $B$ . Since both $A$ and $B$ normalize $B$ , $C=AB$ also normalizes $B$ , so $B$ is normal in $C$ .
2	$B$ normalizes $N$	--	$B$ is abelian	--	[SHOW MORE] Since $N\leq B$ by definition, and $B$ is abelian, so $N$ is normal in $B$ . Thus, $B$ normalizes $N$ .
3	$A$ normalizes $N$	--	$A$ normalizes $B$	--	[SHOW MORE] $A\leq N_{P}(A)$ , so $A$ normalizes $N_{P}(A)$ . Also, $A$ normalizes $B$ . Thus, $A$ normalizes the intersection $N_{P}(A)\cap B=N_{B}(A)$ .
4	$N=N_{B}(A)$ is normal in $C$	--	--	steps (2), (3)	[SHOW MORE] Both $A$ and $B$ normalize $N$ , so $C=AB$ also normalizes $N$ .
5	$N$ is a proper subgroup of $B$	--	$B$ does not normalize $A$		[SHOW MORE] By definition, $N=N_{B}(A)$ normalizes $A$ . If $N=B$ , we'd get that $B$ normalizes $A$ , contrary to assumption.
6	$B/N$ is a nontrivial normal subgroup of $C/N$	fact (3)	--	steps (1), (4), (5)	[SHOW MORE] $C/N$ makes sense by step (4). $B/N$ is normal in it because $B$ is normal in $C$ (step (1)). Finally, $B/N$ is nontrivial because $N$ is a proper subgroup of $B$ (step (3)).
7	$B/N\cap Z(C/N)$ is nontrivial	fact (2)	--	step (6)	Direct combination of the facts
8	Let $x\in P$ be such that its image mod $N$ is a nontrivial element in $B/N\cap Z(C/N)$ . Then $M=[x,A]$ is contained in $N$ and hence in $B$			step (7)	Note that step (7) guarantees the existence of such $x$ . [SHOW MORE] Mod $N$ , $x$ is in the center of $C/N$ , so $[x,A]$ is trivial mod $N$ . Thus, $M=[x,A]\leq N$ . Since $N\leq B$ , $M$ is contained in $B$ .
9	$M=[x,A]$ is an abelian subgroup of $P$		$B$ is abelian	step (8)	[SHOW MORE] By the previous step, $M\leq B$ by assumption, with $B$ abelian. Thus, $M$ , being a subgroup of an abelian group, is abelian.
10	$A^{*}=MC_{A}(M)$ is an abelian subgroup of maximum order in $P$	fact (1)	$A$ is abelian of maximum order	step (9)	Piece together.
11	$A\cap B$ is contained in $C_{A}(M)$		$B$ is abelian	step (8)	[SHOW MORE] Any element of $A\cap B$ centralizes $B$ (since $B$ is abelian). By step (8), $M$ is contained in $B$ , so $A\cap B$ centralizes $M$ . Also, this element is in $A$ , so it is in $C_{A}(M)$ .
12	$A\cap B$ is contained in $A^{*}\cap B$		--	step (11)	[SHOW MORE] By step (11), $A\cap B\leq C_{A}(M)\leq A^{}$ . Since $A\cap B\leq B$ , we get $A\cap B\leq A^{}\cap B$ .
13	$A^{*}$ normalizes $A$			step (8)	[SHOW MORE] Note that $M\leq N=N_{B}(A)$ , so $M$ normalizes $A$ . $C_{A}(M)\leq A$ , with $A$ abelian, so $C_{A}(M)$ normalizes $A$ . Thus, the product $MC_{A}(M)$ normalizes $A$ .
14	$M$ is not contained in $A$			step (8)	[SHOW MORE] By assumption $x\notin N=N_{B}(A)$ , $x$ does not normalize $A$ . Thus, $M=[x,A]$ is not contained in $A$ .
15	$A^{*}\cap B$ is not contained in $A\cap B$			steps (8), (14)	[SHOW MORE] By step (8), $[x,A]=M\leq N\leq B$ , and also $M\leq A^{}$ , so $M\leq A^{}\cap B$ . By step (14), $M$ is not contained in $A$ , and hence, $M$ is not contained in $A\cap B$ . Thus, $A^{*}\cap B$ is not contained in $A\cap B$ .
16	$A^{*}$ is contained in $C=AB$			steps (1), (8), (10)	[SHOW MORE] $A^{*}=MC_{A}(M)$ . By step (8), $M$ is in $B$ and hence in $AB$ . By definition, $C_{A}(M)$ is in $A$ and hence in $AB$ . Thus, the product is in $AB$ .
17	$A^{*}$ is contained in $\langle A^{C}\rangle$ .			steps (8), (9), (10)	[SHOW MORE] A^* = MCA_(M)</math>. $M$ is contained in $\langle A^{C}\rangle$ because it's defined as $[A,x]$ and $x\in C$ . $C_{A}(M)\leq A\leq \langle A^{C}\rangle$ . Thus, the product is also contained in $\langle A^{C}\rangle$ .
18	$A^{*}$ normalizes $B$			step (1), (16)	[SHOW MORE] By step (1), $B$ is normal in $C$ . Since $A^{}\leq C$ by step (16), $A^{}$ thus also normalizes $B$ .

The conclusions of steps (10), (12), (13), (15), (16), (17), and (18) complete the proof.

Conceptual summary of proof

The key idea of the proof is to use fact (1) somehow, and this requires finding a suitable $x$ such that $[x,A]$ is abelian. and the resulting subgroup $A^{*}$ that we get is nice enough.

Working backward from this, we see that we would like that $[x,A]$ not be a subgroup of $A$ , which in turn means that we want $x$ outside $N_{P}(A)$ . On the other hand, we do want $A^{*}$ to normalize $A$ , which means that we want $[x,A]$ to lie inside $N_{P}(A)$ . Finally, we would like $[x,A]\subseteq B$ so that the subsequent group constructed is in $AB$ . With all these considerations, we should aim to find $x$ outside $N_{B}(A)$ but inside $B$ , but such that $[x,A]\subseteq N_{B}(A)$ .

This motivation now allows us to work out the proof details given above. Here is a rough outline of the proof:

Steps (1)-(6) set things up. The fact that $B$ does not normalize $A$ is used to show that $B/N$ is a nontrivial normal subgroup of $P/N$ .
The crucial steps for the construction are (7) and (8), that involve the choice of $M$ . Steps (9) and (10) now use fact (1) to get a hold on $A^{*}$ .
The remaining steps help us get a clearer idea of the subgroup inclusions and prove the remaining desired properties for $A^{*}$ .

GAP implementation

Here is a GAP implementation of the constructive approach used in the proof:

ThompsonsReplacementAbelian := function(P,A,B)
        local C,N,x,M,CAM,Astar;
        C := Group(Union(A,B));
        N := Normalizer(B,A);
        x := Filtered(Set(B),y -> (not(y in N)) and IsSubgroup(N,CommutatorSubgroup(Group(y),C)))[1];
        M := Group(List(Set(A),y -> x^(-1) * y^(-1) * x * y));
        CAM := Centralizer(A,M);
        Astar := Group(Union(M,CAM));
        return Astar;
end;;

References

Textbook references

Finite Groups by Daniel Gorenstein, ISBN 0821843427, Page 273, Theorem 2.5, ^{More info}

Journal references

A replacement theorem for p-groups and a conjecture by John Griggs Thompson, Journal of Algebra, ISSN 00218693, Volume 13, Page 149 - 151(Year 1969): In this paper, Thompson proved the replacement theorem for abelian subgroups, as well as the result that group of prime power order having a larger abelianization than any proper subgroup has class two.^{Official copy}^{More info}
An extension of Thompson's replacement theorem by algebraic group methods by George Glauberman, Finite Groups 2003