The subgroup-coset picture
This is a survey article related to:subgroup
View other survey articles about subgroup
YOU MAY ALSO BE INTERESTED IN: understanding the definition of homomorphism, understanding the quotient map, coset representatives and the axiom of choice, understanding the notions of order and index
While the definition of subgroup may seem disarmingly simple, the large number of results controlling the nature of subgroups in a group, particularly the picture of disjoint cosets of equal size, suggests that there is more to subgroups than meets the eye. This survey article takes a comprehensive look at the picture of subgroups and cosets in a group, and how the axiomatics and structure of groups help in creating this nice picture.
A quick constructive understanding
The left cosets picture
A subgroup of a group is a subset that is closed under the group operations, and hence, forms a group in its own right. One possible definition of a subgroup is as a subset that is closed under the group multiplication, and forms a group itself under the induced multiplication. Another definition of subgroup is as a subset that contains the identity element of the group, and is also closed under the group operations of multiplication and inversion.
From this primitive perspective, there shouldn't be much control that the subgroup has over the other elements of the group. After all, what happens in the subgroup should not affect our ability to add outside symmetries.
Let's suppose we start with a group , and want to construct a bigger group containing . To do that, we need to throw in a new element outside . Suppose we throw in an element . Then, because we want the whole group to be closed under multiplication, we've effectively also thrown in . In other words, we've thrown in the left coset of containing .
So far, we've only used the fact that we have a binary operation. It's now that being a group comes into play. First, we use the fact that since , doesn't meet . That's because if for , then . Inverses and associativity play a crucial role.
Second, we use the fact that the map is bijective. That's because if , then cancellation yields . Again, it is the role of inverses and associativity that allows us to cancel.
Thus, adding a new element adds a left coset that is disjoint from the subgroup, and of the same size. In general, it isn't just sufficient to add one coset -- we may add many more, and what'll happen is that the whole group gets partitioned into left cosets, pairwise disjoint and of the same size as the subgroup. The two key facts we have are:
- Left cosets partition a group (so they're disjoint)
- Left cosets are in bijection via left multiplication (so they have the same size)
What this intuitively tells us is that the left coset is just like the subgroup, translated, as far as its size is concerned.
Left versus right
What we did above using left cosets, can be done equally well using right cosets. The right cosets of a subgroup again partition the group, and are in bijection via right multiplication, so they have the same size. More importantly, using left cosets and right cosets is actually equivalent.
That's because if we consider the map sending every element to its inverse, then the subgroup goes to itself, and every left coset of it goes to a right coset, and every right coset goes to a left coset. So, there's a natural isomorphism between the space of left cosets and the space of right cosets; in particular, they have the same size. The size of either coset space is termed the index of the subgroup. Further information: Left and right coset spaces are naturally isomorphic
Creating a picture
A picture with only the left cosets
Pictures can be particularly dangerous for the intuition, specially in situations where not all structural aspects can be captured using the picture. The ideas here are intended more to provide caution against drawing the wrong kind of picture, rather than to suggest that drawing pictures can provide significant help.
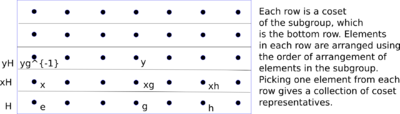
- The first attempt at a picture may be to draw the group as a rectangle, partitioned into rows, where each row represents a left coset of the subgroup. The elements of the group are represented as points in each row.
- For canonicity, we may designate the bottom row as the coset that is the subgroup itself, and the left-most element in the bottom row as the identity element.
- The left-most element in each row is a coset representative for that row (in fact, any element in each row can be designated as a coset representative for that row).
- For convenience, we may order elements in the cosets such that the element in the coset with left-most element , and in the same column as subgroup element , is the element .
- Right multiplication by elements in the subgroup simply causes a permutation of the elements in each row, without interchanging the rows,
- Left multiplication by elements in the group induces a permutation of the rows. It preserves the relation of being in the same row.
What this picture misses out, or may mislead on, are the following:
- The picture may seem to suggest that there is some importance to the columns. Actually, there isn't. In fact, apart from the subgroup itself, where we can choose the identity element as the representative, no other coset comes with a natural choice of representative. Thus, what comes in the left-most column (or what choice of coset representatives we pick) is completely undetermined.
- Further, it may not in general be possible to choose coset representatives to themselves form a subgroup. In other words, the left-most column may not form a subgroup, and there may be no way of choosing things so that it forms a subgroup.
- The picture does not convey any of the complexities of left versus right. For instance, multiplying on the right by an element of the subgroup preserves the rows. But multiplying on the left by an element of the subgroup does not preserve the rows. It preserves the bottom row, but could wreak havoc on the other rows. In other words, if we're thinking of the action of the group on the coset space by left multiplication, the subgroup does not in general preserve every row.
To get a better understanding, we need to look at important concepts: conjugate subgroups, normal core, normal closure and normalizer, and we'll then be able to incorporate more into the picture.
Isotropy, grouping, normalizer, and normal closure
Suppose is a subgroup and is a left coset of . Then, the subgroup of comprising those such that , is not necessarily equal to . However, it is related to in a simple fashion: it is the conjugate .
(This is related to fundamental theorems about group actions and isotropy, and can be checked easily).
Thus, the possible isotropy sugbroups (stabilizers) of the cosets under left multiplication by , are the conjugate subgroups to . This suggests a slight redrawing of the picture:
- Earlier, our ordering of the rows representing cosets was arbitrary. Now, we do a slightly more careful ordering of the rows: we group together those cosets that have the same isotropy. In particular, the bottom grouping of rows comprises those for which , or equivalently, . The bottom grouping comprises those left cosets of that are also right cosets of . Equivalently, the elements there are the satisfying , and this is a subgroup called the normalizer of in . This subgroup is denoted .
- All the other groupings of rows have the same size as the bottom grouping. In fact, each grouping of rows, i.e., each collection of cosets that have the same isotropy subgroup, is a left coset of in .
- Earlier, we had complained that multiplication by on the left doesn't preserve each row. But now, we know, for each grouping, the conjugate of that preserves that grouping. So, we also know the subgroup that preserves everything: it is the intersection of all conjugate subgroups of , also called the normal core of . This can be depicted by writing the stabilizer for each grouping of cosets, and then clubbing them all together to write the grand intersection, which is the normal core of .
Some particular subgroup properties
Normal subgroup
Further information: Normal subgroup
A subgroup of a group is normal in if for all . If is normal in , we have the following:
- The isotropy subgroup of every coset is precisely . Thus, according to our earlier idea of grouping the rows in such a way that the ones with the same isotropy subgroup occur together, we just get a single grouping of all the rows.
- The normal core, i.e., the subgroup that preserves every row, is the same as . In other words, acts as the identity on under left multiplication.
Self-normalizing subgroup
Further information: Self-normalizing subgroup
A subgroup of a group is termed self-normalizing in if it equals its normalizer in . Equivalently, if and only if .
For a self-normalizing subgroup, any two distinct left cosets of have distinct isotropy subgroups. Thus, there are as many conjugate subgroups as there are cosets.
Core-free subgroup
Further information: Core-free subgroup
A subgroup of a group is termed core-free in if the action of on by left multiplication is faithful, i.e., no non-identity element of preserves every left coset.
As discussed above, the elements of that preserve every left coset of are precisely the elements in every conjugate subgroup of . This intersection is termed the normal core of . Thus, is core-free if and only if the normal core of is a subgroup.
Permutably complemented subgroup
Further information: Permutably complemented subgroup
Two subgroups and of a group are termed permutable complements if and is trivial. Note that if , then . Thus, forms a left transversal of in .
We may want to redraw the subgroup-coset picture such that the elements of form the left-hand column. This is related to the view of as having a -coordinate and a -coordinate: the horizontal coordinate represents the -coordinate, and the vertical coordinate represents the -coordinate. We thus get a set-theoretic bijection:
given by:
.
The reverse map takes an element of and writes it uniquely as the product of its coset representative and an element of .
However, this bijection is not an isomorphism between and the external direct product of and , because need not equal . In fact, it is an isomorphism only if both and are normal subgroups. In this case, we say that is an internal direct product of and .
Note that:
- There may be no canonical choice of permutable complement to a subgroup, even if a permutable complement exists.
- There may be non-isomorphic choices of permutable complements to in . In fact, any two finite groups of the same order can occur as permutable complements to the same subgroup in a group. Further information: Every group of given order is a permutable complement for symmetric groups
Complemented normal subgroup and retract
Further information: Permutably complemented normal subgroup, retract
We now consider the situation where is normal and has a permutable complement . We say that is a permutably complemented normal subgroup of and that is a retract of . In this case, we still have a set-theoretic bijection:
given by:
.
As before, the map need not be an isomorphism in the group-theoretic sense. However, it turns out that the projection from to is a homomorphism. In fact, it is an idempotent homomorphism: its restriction to is the identity map. Such homomorphisms are termed retractions, and we thus say that is a retract of .
Note also that is isomorphic to the quotient group . Thus, unlike the non-normal case, any two permutable complements to a normal subgroup must be isomorphic.
Direct factor
Further information: Internal direct product, External direct product, Direct factor
When and are both normal in , then the map:
given by , is an isomorphism from the external direct product to . In this case, we say that is an internal direct product of subgroups and .
In this case, the subgroup-coset picture is fairly accurate: the bottom row represents elements of , the left column represents elements of . To multiply two elements of , we project them on their rows and columns, multiply the projections in and respectively, and multiply back.
Further, is isomorphic to , so the isomorphism type of is completely determined.
However, as before, itself is not necessarily uniquely determined by .
Some worked-out examples
PLACEHOLDER FOR INFORMATION TO BE FILLED IN: [SHOW MORE]
































