Understanding the cycle decomposition
This is a definition understanding article -- an article intended to help better understand the definition(s):cycle decomposition for permutations
View other definition understanding articles| View other survey articles about cycle decomposition for permutations
A permutation on a set is a bijective map from to itself. The permutations on a set form a group under composition; this group is termed the symmetric group.
There are many ways of describing permutations: one way is to give a formula for the function; another is to write the permutation down using the one-line or two-line notation. However, these ways of writing permutations down often fail to provide a feel for the dynamics of a permutation, and its group-theoretic nature.
The cycle decomposition of a permutation is a form of expressing the permutation that captures its dynamics as well as its group-theoretic behavior. This survey article builds the idea of cycle decompositions in a number of ways, and provides some useful examples.
To get a full list of cycle decompositions of permutations written alongside the one-line notation, see element structure of symmetric group:S3#Elements and element structure of symmetric group:S4#Elements.
The directed graph associated with a function
Description of the directed graph
Suppose is a set and is a function. We define the directed graph associated with as follows.
- The vertices, or points, or nodes, of the graph are the elements of . In other words, we begin by drawing all the elements of as separate points.
- There is a directed edge from a vertex to a vertex if and only if . Note that if , we get a directed edge from to itself -- this is called a loop.
Notice the following:
- Since is a function, there is a unique value of for every . Thus, there is a unique directed edge coming out from , and this edge is headed towards .
- The edges coming to represent all the points such that .
- is injective if and only if, for every , there is at most one edge entering .
- is surjective if and only if, for every , there is at least one edge entering .
- is bijective if and only if, for every , there is exactly one edge entering .
Finite examples
Suppose is the set and the function is defined by:
.
The directed graph associated with looks like this:
Notice that is neither injective nor surjective. Both and map to , leading to the vertex having an indegree of two -- two incoming edges. On the other hand, the vertex has an indegree of zero -- there are no incoming edges to this vertex.
In contrast, consider the function:
.
This function is bijective, and the graph clearly shows this:
Infinite examples
In the infinite case, there are examples of functions that are injective and not surjective, and there are also examples of functions that are surjective but not injective. Here are some, along with finite fragments of their graphs:
- The function on the set of integers. This is injective, but not surjective: its image is the set of even integers. The picture makes this clear.
- The function that sends to if is even and to if is odd. This is surjective (every element is the image of its double) but is not injective (the odd numbers have two incoming edges).
The inverse of a bijective function
If is bijective, i.e., is a permutation, the directed graph associated with has the property that every vertex has indegree one and every vertex has outdegree one. Further, there is a simple relation between the graph of and the graph of .
For any , is the unique satisfying . In other words, it is the starting point of the directed edge that ends at . This suggests that if we reverse the direction of the edge, we get an edge sending to .
The upshot: given a bijective function, the directed graph of the inverse function is obtained by simply reversing the direction on all edges in its directed graph.
Iteration and dynamics
Another advantage of the directed graph is that it helps see what happens on iterating the function. To understand this, recall that to know , we need to start at and flow along the unique edge emanating from . Thus, to find , we need to first reach , and then flow along the unique edge emanating from that point. More generally, to find , we need to start at and move forward steps along the edges of the graph.
The cycle decomposition: how it can loop back
We already understand the local picture for the directed graph associated with a permutation. Let's try to understand the implications of this picture more closely.
Suppose is a permutation (i.e., a bijective function). Suppose I start at a point and consider the sequence of points . Essentially, I start at the point and move forward along the edges of the graph.
Notice the following: if I ever repeat a point, the first point I repeat must be . To see this, observe that if , and , then , and the injectivity of yields that . A downward induction thus shows that .
This can also be seen pictorially: the graph cannot loop back to a point other than , because this point already has an incoming edge. Thus, the graph must loop back to itself, or not loop back at all.
Note that when is not injective, the graph can cycle back to a point other than , giving a classic shape.
The cycle decomposition: cycles or chains
When is a finite set and is a permutation of , we know that if we start moving along from any vertex along the graph, we'll eventually repeat a vertex. The remarks made above thus show that we get a cycle at .
When is infinite, cycles are not the only possibility. It is also possible that applying repeatedly never returns to the original point. An example is the translation map on the group of integers: the map . Here, iterating the permutation keeps the point moving to the right, and there is no looping back.
If there is no looping back, we can also go backward for an infinite duration without looping back. For instance, for the map , for which there is no looping back, the inverse map also has no looping back. Thus, instead of a cycle, we obtain a straight chain extending indefinitely in both directions.
Note that for an injective map (as opposed to a bijective map) there may exist chains that extend indefinitely in the forward direction, but can be extended only to a finite extent in the backward direction. An example is the map on the set of positive integers.
The cycle decomposition: obtaining the decomposition
Further information: cycle decomposition theorem for permutations
We've seen that starting from any element , we can trace either a cycle or a chain containing , obtained by following the flow of the edges. Explicitly, the cycle of gives, in (cyclic) sequence the points .
Since every element has its own unique cycle or chain, the cycles and chains form a partition of the whole set . In the finite case, there are no chains, so the set is partitioned as a union of disjoint cycles.
Here is another way of thinking about the cycle decomposition. We start with a point and trace the cycle of . Note that for any point in the cycle of , the cycle of that point is the same as the cycle of . Now, if the cycle contains all points of , we are done. Otherwise, pick a point not in the cycle, and trace its cycle. This cycle cannot intersect the previous cycle, since that would contradict the fact that there is a unique edge coming into every vertex. Thus, we get a new cycle, that covers some new elements. We repeat this process until the whole finite set is covered.
In infinite sets, this repeat until idea cannot be used in a naive sense, but the more sophisticated idea of being in the same cycle as an equivalence relation works.
Some easy examples
Integers modulo seven with some polynomial maps
Let be the group of integers modulo seven under addition. In other words, we have:
.
Suppose is the map:
.
We want to determine the cycle decomposition for .
First, we compute the images of all the elements of under . We have:
Notice that the cycle decomposition makes clearly visible some things that are not so obvious otherwise: there is exactly one fixed point (the element , which has a loop around it) and there are two cycles of size three each.
Here's another map:
For this, we obtain:
.
We now make the cycle decomposition:
From the cycle decomposition, we see that there is a 4-cycle and a 3-cycle .
Writing the cycle decomposition
Writing each cycle
Each cycle is written in parentheses, with the members of the cycle written in cyclic order. In other words, the image of any member under the permutation is the next member, and the image of the right-most member is the left-most member. The cycle decomposition involves juxtaposing the expressions for each of the cycles.
The individual members of the cycle are preferably separated by commas, although some abbreviated conventions allow for simply writing the members without separating symbols.
For instance, the permutation described above on the set :
The cycle decomposition of this is written as:
The order in which the individual cycles are written does not matter, so this is the same as:
or:
.
Finally, within each cycle, the ordering of elements can be permuted cyclically, so can be rewritten as . However, it is not the same as , because the latter sends to , rather than to .
For the second example:
we can write the cycle decomposition as:
.
Thus, there are two sources of ambiguity in the expression for the cycle decomposition:
- The ordering between cycles is immaterial -- any ordering is fine.
- Within a cycle, the choice of which element to start the cycle with is arbitrary. Once the left-most element of the cycle is chosen, subsequent elements are decided (because each is the image of its predecessor).
Omission of fixed points
When writing the cycle decomposition, we can omit cycles of size 1, i.e., fixed points. Thus, the permutation above:
can be written as:
Computation using cycle structure
Cycle type of a permutation
Further information: cycle type of a permutation, cycle type determines conjugacy class
The cycle type of a permutation is the information comprising the sizes of its cycles. For instance, if a permutation has two cycles of size three and one cycle of size one, we say that it has cycle type .
Note that the cycle type of a permutation corresponds to an unordered tuple of natural numbers that add up to the total size of the set. Thus, it corresponds to an unordered integer partition of the size of the set. In particular:
Cycle types of permutations on a set Unordered integer partitions of the size of the set
A few things should be noted carefully:
- The cycle type is unordered. Thus, a cycle type of is the same as a cycle type of or .
- What really matters in the cycle type is the number of cycles of each size. Thus, we can store the information of the cycle type as an ordered list where that member is the number of cycles of size . (This point is a little tricky). For instance, a cycle type of can be stored using the ordered list , indicating that there is one cycle of size one, zero cycles of size two, and two cycles of size three.
Computing the powers of a permutation
The cycle structure of a permutation is a very convenient tool for computing its powers. For instance, to compute the power of a permutation, we simply start at a vertex, and flow along the arrows in its cycles steps. To compute the inverse of a permutation, we go backward along the cycle.
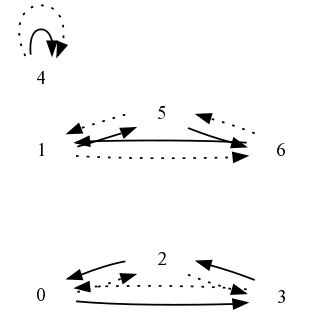
For instance, the dotted lines below demonstrate the cycle decomposition of the inverse permutation to our first example:
Thus we get:
Note that fixed points remain fixed points, so they do not need to be written on either side.
Next, we show how the square of the second permutation is computed, with the dotted arrows representing the cycle decomposition of the square permutation:
In symbols, we have:
Computing the order of a permutation
The order of a permutation is the least common multiple of the orders of all the cycles that comprise that permutation. To see this, note that for the power of a permutation to be the identity map, it should cycle each element back to itself.
For instance, the first permutation has a cycle decomposition with cycles of sizes , so the order is . For the second permutation, the cycles have sizes and , so the order is .