Element structure of modular maximal-cyclic group:M16
This article gives specific information, namely, element structure, about a particular group, namely: M16.
View element structure of particular groups | View other specific information about M16
To describe subgroups, we use the defining presentation given here:
with denoting the identity element.
This is a group of order 16, with elements:
Conjugacy and automorphism class structure
Conjugacy class structure
FACTS TO CHECK AGAINST FOR CONJUGACY CLASS SIZES AND STRUCTURE:
Divisibility facts: size of conjugacy class divides order of group | size of conjugacy class divides index of center | size of conjugacy class equals index of centralizer
Bounding facts: size of conjugacy class is bounded by order of derived subgroup
Counting facts: number of conjugacy classes equals number of irreducible representations | class equation of a group
| Conjugacy class | Size of conjugacy class | Order of elements in conjugacy class | Centralizer of first element of class |
|---|---|---|---|
| 1 | 1 | whole group | |
| 1 | 2 | whole group | |
| 1 | 4 | whole group | |
| 1 | 4 | whole group | |
| 2 | 8 | ||
| 2 | 8 | ||
| 2 | 2 | ||
| 2 | 4 | ||
| 2 | 8 | ||
| 2 | 8 |
Automorphism class structure
| Equivalence class under automorphisms | Size of equivalence class | Number of conjugacy classes in it | Size of each conjugacy class | Characterization(s) up to 1-isomorphism | Characterization(s) involving commutation relationships |
|---|---|---|---|---|---|
| 1 | 1 | 1 | identity element | identity element | |
| 1 | 1 | 1 | unique non-identity element that is a fourth power | unique non-identity element that is a commutator | |
| 2 | 2 | 1 | squares that are not fourth powers | elements in the center but not in the derived subgroup | |
| 8 | 4 | 2 | elements of order eight | ||
| 2 | 1 | 2 | elements of order two that are not squares | ||
| 2 | 1 | 2 | elements of order four that are not squares |
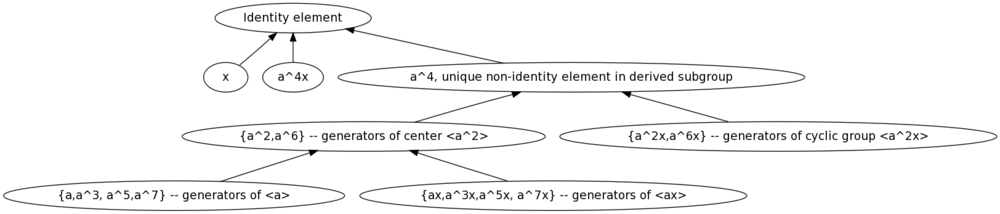
Endomorphism structure
The bubbles here correspond to equivalence classes under automorphisms. The arrows here indicate that there is an endomorphism taking an element in one bubble to an element in the other bubble. To avoid confusion, we do not draw all arrows, we draw enough that taking the transitive closure generates all possible arrows.
Order and power information
Directed power graph
Below is a collapsed version of the directed power graph of the group. Here, each node represents an equivalence class of elements under the relation of generating a given cyclic subgroup. An edge from one node to occurs if some element in the latter node is the square of some element in the former node. We remove the loop at the identity element.
1-isomorphism
The group is 1-isomorphic to direct product of Z8 and Z2. In particular, the directed power graphs of the two groups are isomorphic as graphs. This 1-isomorphism is a special case of a general version of the Baer correspondence, which in turn is a special case of a Lazard correspondence. See proof of generalized Baer construction of Lie ring for class two 2-group with a suitable cocycle.
For more on the specific 1-isomorphism, refer Baer correspondence between M16 and direct product of Z8 and Z2.
Order statistics
| Number | Elements of order exactly that number | Number of such elements | Number of conjugacy classes of such elements | Number of elements whose order divides that number | Number of conjugacy classes whose element order divides that number |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | |
| 2 | 3 | 2 | 4 | 3 | |
| 4 | 4 | 3 | 8 | 6 | |
| 8 | 8 | 4 | 16 | 10 |
Power statistics
| Number | powers that are not powers for any larger divisor of the group order | Number of such elements | Number of conjugacy classes of such elements | Number of powers | Number of conjugacy classes of powers |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 16 | 10 | |
| 2 | 2 | 2 | 4 | 4 | |
| 4 | 1 | 1 | 2 | 2 | |
| 8 | -- | 0 | 0 | 1 | 1 |
| 16 | 1 | 1 | 1 | 1 |