D8 versus Q8
This survey article compares, and contrasts, the following: dihedral group:D8 versus quaternion group
View other comparison survey articles View survey articles related to dihedral group:D8 View survey articles related to quaternion group
The dihedral group of order eight, and the quaternion group, are both similar and different in a number of ways. They are the smallest, and simplest, examples of non-Abelian 2-groups, and more generally, of non-Abelian nilpotent groups. They generalize respectively to the families of dihedral groups and dicyclic groups, and the two families are both similar and different in a number of ways.
In this article, we'll study the similarities and differences between these two groups, in terms of the subgroup structure, automorphisms, linear representations, and other places where the groups occur.
Subgroup structure
Both are extraspecial of order eight
Both the groups are of order eight, and are extraspecial groups. In other words, for both groups, the center equals the commutator subgroup equals the Frattini subgroup, and is cyclic of order two. In the quaternion group, the center comprises the elements , while in the dihedral group, the center comprises the identity, and rotation by .
In the quaternion group, every subgroup contains the center
In the quaternion group, every nontrivial subgroup contains the center. In fact, there's a total of only six subgroups: the trivial subgroup, the whole group, the center, and three cyclic subgroups of order four.
In the dihedral group, there are many subgroups of order two that do not contain the center, namely: the four subgroups generated by the four reflections. Thus, the dihedral group has a total of ten subgroups: the trivial subgroup, the whole group, the center, the four two-element subgroups generated by reflections, and three four-element subgroups.
This gives a pretty different feel to the lattices of subgroups of the two groups, as can be seen from the pictures of the lattices.

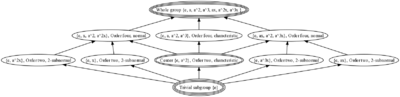
The three subgroups of order four
In the quaternion group, the three subgroups of order four are all cyclic. Moreover, they are automorphic subgroups: there is an outer automorphism taking any of them to any other.
For the dihedral group, there are three subgroups of order four, one of which is cyclic, and the other two are elementary Abelian (isomorphic to the Klein four-group). The cyclic subgroup (the one comprising rotations) is characteristic, while the two elementary Abelian subgroups are automorphs of each other.
Decomposition as a semidirect product
The quaternion group is a splitting-simple group: it does not split as an internal semidirect product of smaller subgroups. This is related to the fact that every nontrivial subgroup contains the center.
The dihedral group is the semidirect product of its cyclic subgroup of order four, and any two-element subgroup generated by a reflection. It can also be expressed as the semidirect product of an elementary Abelian subgroup of order four, and a two-element subgroup generated by a reflection outside that elementary Abelian subgroup.
In fact, in the dihedral group, every subgroup apart from the center is permutably complemented.
Automorphism structure
The automorphisms of the quaternion group are isomorphic to the symmetric group on four letters (which has order 24). These automorphisms act transitively on the six elements . The automorphism group has a normal subgroup of order four, isomorphic to a Klein four-group, that acts trivially on the Abelianization.
The dihedral group has considerably fewer automorphisms. This is also related to the fact that it has a greater variety of subgroups, and fewer automorphisms taking one kind of subgroup to another. In fact, the automorphism group of the dihedral group is again isomorphic to the dihedral group, with the action by conjugation mapping the dihedral group to a Klein four-subgroup of the other dihedral group.
Linear representations
The character table of the dihedral group and of the quaternion group are identical, and so are the conjugacy class sizes in the two groups. Both are rational groups: all the characters are integer-valued.
There is one important difference between the two groups. While the dihedral group has the property that all its representations are themselves realized over the rationals, the irreducible two-dimensional representation of the quaternion group cannot be realized over the rationals. Thus, the quaternion group is a rare example of a rational group that is not a rational-representation group.



