2-subnormality is not finite-join-closed

This article gives the statement, and possibly proof, of a subgroup property (i.e., 2-subnormal subgroup) not satisfying a subgroup metaproperty (i.e., finite-join-closed subgroup property).This also implies that it does not satisfy the subgroup metaproperty/metaproperties: Join-closed subgroup property (?), .
View all subgroup metaproperty dissatisfactions | View all subgroup metaproperty satisfactions|Get help on looking up metaproperty (dis)satisfactions for subgroup properties
Get more facts about 2-subnormal subgroup|Get more facts about finite-join-closed subgroup propertyGet more facts about join-closed subgroup property|

Statement

A join of two 2-subnormal subgroups of a group need not be 2-subnormal.

Related facts

• 2-subnormal implies join-transitively subnormal: The join of a 2-subnormal subgroup and a $k$-subnormal subgroup is $2k$-subnormal. In particular, the join of two 2-subnormal subgroups is 4-subnormal, and a join of $r$ 2-subnormal subgroups is $2^{r}$-subnormal.
• Normal implies join-transitively 2-subnormal, and more generally, join of normal and subnormal implies subnormal of same depth: A join of a normal subgroup and a 2-subnormal subgroup is 2-subnormal. More generally, the join of a normal subgroup and a $k$-subnormal subgroup is $k$-subnormal.

Proof

Example of a group of order $64$

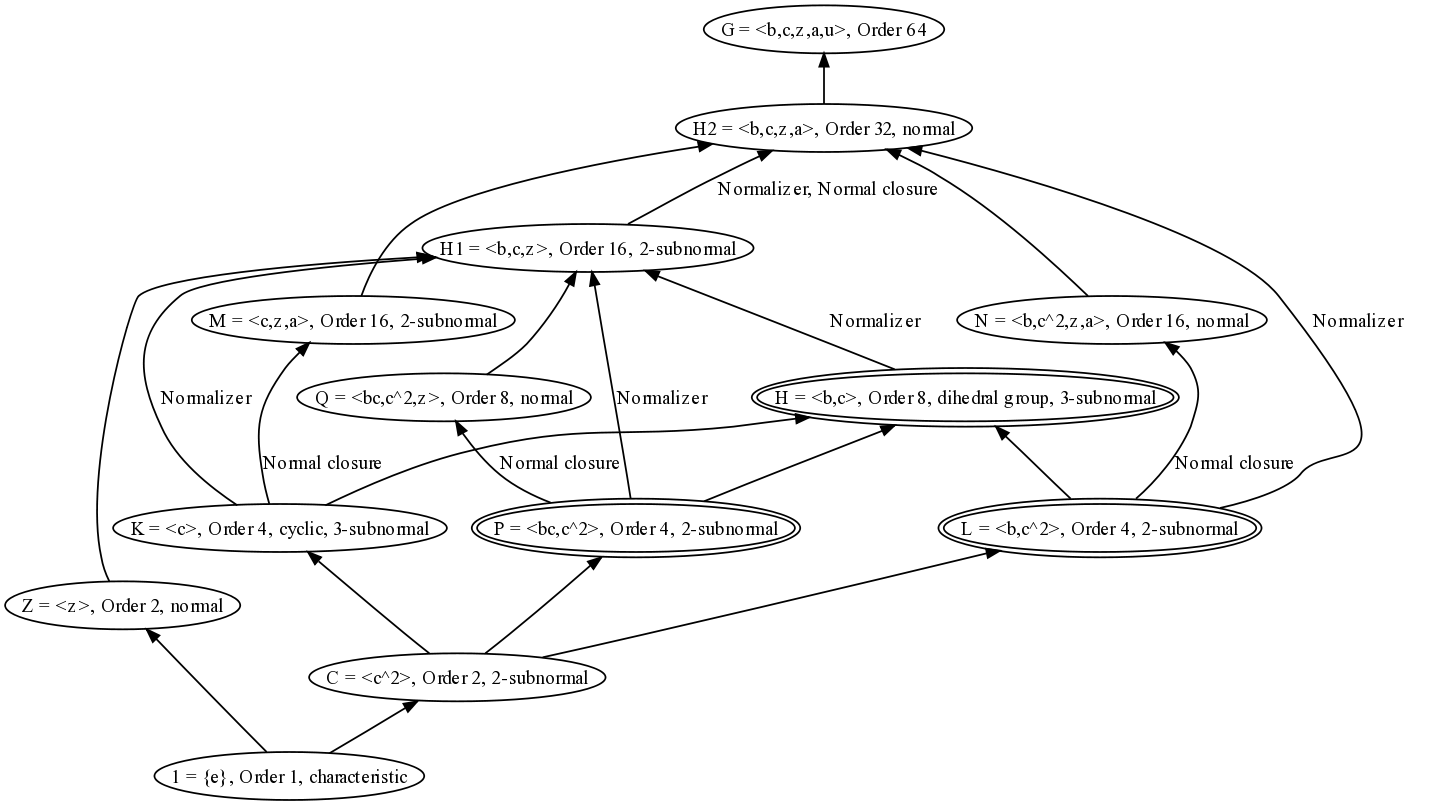
We discuss here the example of a group of order 64, given as follows (here $e$ denotes the identity element):

$G=\langle c,b,z,a,u\mid c^{4}=e,b^{2}=e,bcb^{-1}=c^{3},z^{2}=e,zcz^{-1}=c,zbz^{-1}=b,a^{2}=e,aca^{-1}=cz,aba^{-1}=b,u^{2}=bc,ucu^{-1}=c^{3}za,uau^{-1}=c^{2}za\rangle$

The two 2-subnormal subgroups are $P=\langle bc,c^{2}\rangle$ and $L=\langle b,c^{2}\rangle$, and their join, which is $H=\langle b,c\rangle$, is 3-subnormal but not 2-subnormal.

Note that the GAP ID of $G$ is $(64,32)$: it is the $32^{nd}$ among GAP's list of groups of order $64$.

The lattice of the relevant subgroups of $G$ is depicted in the diagram below:

Let's go over this step by step:

• The subgroup $\langle c,b\rangle$ is a dihedral group, which we call $H$. This has three subgroups of order four: the subgroup $K=\langle c\rangle$, the subgroup $P=\langle bc,c^{2}\rangle$, and the subgroup $L=\langle b,c^{2}\rangle$. What happens is that $H$ is 3-subnormal, whereas both subgroups $P$ and $L$ are 2-subnormal.
• $H$ is 3-subnormal but not 2-subnormal: In fact, $H$ has a subnormal series $H\leq H_{1}\leq H_{2}\leq G$, where $N_{G}(H)=H_{1},N_{G}(H_{1})=H_{2},N_{G}(H_{2})=G$. Here, $H_{1}=\langle b,c,z$ and $H_{2}=\langle b,c,z,a$. This is both the fastest ascending and the fastest descending subnormal series: the normal closure of $H$ in $G$ is $H_{2}$, and the normal closure of $H$ in $H_{2}$ is $H_{1}$. Note that the presentation is given in a way that fits this subnormal series well.
• $P$ is 2-subnormal: This needs careful understanding: the normalizer of $P$ in $G$ is $H_{1}=\langle b,c,z\rangle$, and this is not normal in $G$. (Thus, $P$ is not a 2-hypernormalized subgroup). Nonetheless, $P$ is 2-subnormal, because the normal closure of $P$, defined as $Q=\langle bc,c^{2},z\rangle$, is contained in the normalizer.
• $L$ is 2-subnormal: The normalizer of $L$ in $G$ is $H_{2}$, while its normal closure is the subgroup $N=\langle b,c^{2},z,a\rangle$. Since the normal closure is contained in the normalizer, $L$ is 2-subnormal. Note that in this case, it is also true that $L$ is a 2-hypernormalized subgroup: the normalizer of $L$ is normal in $G$.