Subgroup structure of groups of order 8

This article gives specific information, namely, subgroup structure, about a family of groups, namely: groups of order 8.
View subgroup structure of group families | View subgroup structure of groups of a particular order |View other specific information about groups of order 8

The list

Group	Second part of GAP ID	Subgroup structure page	Lattice of subgroups picture
Cyclic group:Z8	1	subgroup structure of cyclic group:Z8
Direct product of Z4 and Z2	2	subgroup structure of direct product of Z4 and Z2
Dihedral group:D8	3	subgroup structure of dihedral group:D8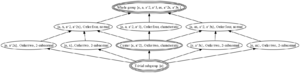
Quaternion group	4	subgroup structure of quaternion group
Elementary abelian group:E8	5	subgroup structure of elementary abelian group:E8

Subgroup/quotient relationships

Subgroup relationships

Quotient relationships

Numerical information on counts of subgroups by isomorphism type

FACTS TO CHECK AGAINST FOR SUBGROUP STRUCTURE: (group of prime power order)
Lagrange's theorem (order of subgroup times index of subgroup equals order of whole group, so all subgroups have prime power orders)|order of quotient group divides order of group (and equals index of corresponding normal subgroup, so all quotients have prime power orders)
prime power order implies not centerless | prime power order implies nilpotent | prime power order implies center is normality-large
size of conjugacy class of subgroups divides index of center
congruence condition on number of subgroups of given prime power order: The total number of subgroups of any fixed prime power order is congruent to 1 mod the prime.

Number of subgroups per isomorphism type

The number in each column is the number of subgroups in the given group of that isomorphism type:

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	cyclic group:Z2	cyclic group:Z4	Klein four-group	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z8	1	3	$(3)$ 1	1	0	4
direct product of Z4 and Z2	2	2	$(21)$	3	2	1	8
dihedral group:D8	3	4	$8\Gamma _{2}a_{1}$	5	1	2	10
quaternion group	4	5	$8\Gamma _{2}a_{2}$	1	3	0	6
elementary abelian group:E8	5	1	$(1^{3})$	7	0	7	16

Number of conjugacy classes of subgroups per isomorphism type

The number in each column is the number of conjugacy classes of subgroups in the given group of that isomorphism type:

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	cyclic group:Z2	cyclic group:Z4	Klein four-group	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z8	1	3	$(3)$ 1	1	0	4
direct product of Z4 and Z2	$(21)$	2	2	3	2	1	8
dihedral group:D8	3	4	$8\Gamma _{2}a_{1}$	3	1	2	8
quaternion group	4	5	$8\Gamma _{2}a_{2}$	1	3	0	6
elementary abelian group:E8	5	1	$(1^{3})$	7	0	7	16

Number of normal subgroups per isomorphism type

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	cyclic group:Z2	cyclic group:Z4	Klein four-group	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z8	1	3	$(3)$	1	1	0	4
direct product of Z4 and Z2	2	2	$(21)$	3	2	1	8
dihedral group:D8	3	4	$8\Gamma _{2}a_{1}$	1	1	2	6
quaternion group	4	5	$8\Gamma _{2}a_{2}$	1	3	0	6
elementary abelian group:E8	5	1	$(1^{3})$	7	0	7	16

Number of automorphism classes of subgroups per isomorphism type

The number in each column is the number of automorphism classes of subgroups in the given group of that isomorphism type:

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	cyclic group:Z2	cyclic group:Z4	Klein four-group	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z8	1	3	$(3)$	1	1	0	4
direct product of Z4 and Z2	2	2	$(21)$	2	1	1	6
dihedral group:D8	3	4	2	$8\Gamma _{2}a_{1}$	1	1	6
quaternion group	4	5	$8\Gamma _{2}a_{2}$	1	1	0	4
elementary abelian group:E8	5	1	$(1^{3})$	1	0	1	4

Number of characteristic subgroups per isomorphism type

Group	Second part of GAP ID	Hall-Senior number	Hall-Senior symbol	cyclic group:Z2	cyclic group:Z4	Klein four-group	Total (row sum + 2, for trivial group and whole group)
cyclic group:Z8	1	3	$(3)$	1	1	0	4
direct product of Z4 and Z2	2	2	$(21)$	1	0	1	4
dihedral group:D8	3	4	$8\Gamma _{2}a_{1}$	1	1	0	4
quaternion group	4	5	$8\Gamma _{2}a_{2}$	1	0	0	3
elementary abelian group:E8	5	1	$(1^{3})$	0	0	0	2

Numerical information on counts of subgroups by order

Number of subgroups per order

Note that by the congruence condition on number of subgroups of given prime power order, all the counts of total number of subgroups as well as number of normal subgroups are congruent to 1 modulo the prime $p=2$, and hence are odd numbers.

Group	Second part of GAP ID	Hall-Senior number	Subgroups of order 2	Normal subgroups of order 2	Subgroups of order 4	Normal subgroups of order 4
cyclic group:Z8	1	3	1	1	1	1
direct product of Z4 and Z2	2	2	3	3	3	3
dihedral group:D8	3	4	5	1	3	3
quaternion group	4	5	1	1	3	3
elementary abelian group:E8	5	1	7	7	7	7

Number of abelian subgroups per order

This is identical to the above table, because all groups of order 2 or 4 are abelian.

Possibilities for maximal subgroups

Collection of isomorphism classes of maximal subgroups	Groups
cyclic group:Z4 only	cyclic group:Z8, quaternion group
Klein four-group only	elementary abelian group:E8
cyclic group:Z4 and Klein four-group	direct product of Z4 and Z2, dihedral group:D8